INTEGRATED ARITHMETIC AND ALGEBRA
Unit 10 Radical Expressions
General Outcome:
10.0 The student shall be able to identify, simplify, and perform operations of addition and subtraction on radical expressions.
Specific Measurable Learning Outcomes:
Upon successful completion of this unit, the student shall be able to:
10.1 Define the terms “square root,” “radical,” and “radicand.”
10.2 Define the terms “nth root” and “index.” (OPTIONAL)
10.3 Simplify square root numerical expressions.
10.4 Determine approximate square roots of numerical expressions.
10.5 Explain why the square root of a negative number is not real.
10.6 Simplify nth root numerical expressions. (OPTIONAL)
10.7 Explain why any even root of a negative number is not real. (OPTIONAL)
10.8 Simplify square root variable expressions.
10.9 Simplify nth root variable expressions. (OPTIONAL)
10.10 Add & subtract square root expressions.
10.11 Add & subtract higher-order radical expressions with identical indices. (OPTIONAL)
10.12 Explain what the Pythagorean Theorem says and means.
10.13 Solve appropriate word problems using the Pythagorean Theorem.
Unit 11 Geometric Calculations, Charts, and Graphs
General Outcome:
11.0 The student shall be able to name and calculate various measurements associated with basic two-dimensional shapes without the aid of a calculator, and interpret data illustrated on bar graphs, line graphs, and pie charts without the aid of a calculator.
Specific Measurable Learning Outcomes:
Upon successful completion of this unit, the student shall be able to:
11.1 Identify a triangle, parallelogram, rectangle, square, trapezoid and circle.
11.2 Define the terms “perimeter,” “area,” “radius,” “diameter,” and “circumference.”
11.3 Calculate the perimeter of triangles, parallelograms, rectangles, squares, and trapezoids (with appropriate units).
11.4 Approximate π to at least 2 decimal places.
11.5 Calculate the circumference of circles (with appropriate units).
11.6 Calculate the area of triangles, parallelograms, rectangles, squares, trapezoids, and circles (with appropriate units).
11.7 Identify a bar graph, and analyze and interpret data illustrated by a bar graph.
11.8 Identify a line graph, and analyze and interpret data illustrated by a line graph.
11.9 Identify a pie chart, and analyze and interpret data illustrated by a pie chart.
Unit 12 Measurements and Unit Analysis
General Outcome:
12.0 The student shall be able to identify and convert among units of measurement without the aid of a calculator.
Specific Measurable Learning Outcomes:
Upon successful completion of this unit, the student shall be able to:
12.1 Recognize standard U.S. system units of length, area, volume, and weight.
12.2 Convert between different U.S. system units for a given measurement using unit analysis.
12.3 Recognize standard metric system units of length, area, volume, and weight.
12.4 Convert between different metric system units for a given measurement using decimal-point translation. (OPTIONAL)
12.5 Given the conversion factors, convert between U.S. system and metric system units for a given measurement using unit analysis.
12.6 Convert between the Celsius and Fahrenheit units of temperature
measurement.
(OPTIONAL)
Unit 13 The Rectangular Coordinate System
General Outcome:
13.0 The student shall be able to (1) identify the quadrants of the rectangular coordinate system, (2) plot points corresponding to ordered-pair coordinates, and (3) identify the ordered-pair coordinates of points plotted on the rectangular coordinate system.
Specific Measurable Learning Outcomes:
Upon successful completion of this unit, the student shall be able to:
13.1 Identify and draw the rectangular coordinate system axes.
13.2 Identify and name each quadrant of the rectangular coordinate system.
13.3 Define the term “origin,” and identify the origin of the rectangular coordinate system.
13.4 Plot points on the rectangular coordinate system representing given ordered-pair coordinates.
13.5 Plot points on the axes representing given ordered-pair coordinates.
13.6 Give the ordered-pair coordinates of points plotted on the rectangular coordinate system.
Unit 14 Lines, Slope, & Graphical Solutions to Systems of Linear Equations
General Outcome:
14.0 The student shall be able to (1) evaluate and interpret the slope of a line, (2) graph lines given two points or a point and the slope, (3) use the slope to determine additional points on a line, (4) graph horizontal and vertical lines, and (5) determine the solution to a system of linear equations graphically.
Specific Measurable Learning Outcomes:
Upon successful completion of this unit, the student shall be able to:
14.1 Explain what it means to be a solution to an equation in two variables.
14.2 Determine if a given ordered pair is a solution to an equation in two variables.
14.3 Define the terms “x- (or horizontal) intercept” and “y- (or vertical) intercept.”
14.4 Sketch the graphs of linear equations in two variables given any two points.
14.5 Sketch the graphs of linear equations in two variables given the x- and y- intercepts.
14.6 Identify and determine the x- and y-intercepts of graphs of linear equations of two variables.
14.7 Sketch horizontal and vertical lines using their equations.
14.8 Determine the equations of horizontal and vertical lines.
14.9 Define the term “slope.”
14.10 Evaluate the slopes of horizontal, vertical, and diagonal lines.
14.11 Interpret the practical meaning of slope in appropriate word problems.
14.12 Sketch graphs of linear equations in two variables given any point and the slope.
14.13 Use the slope to determine additional points on the graphs of lines.
14.14 Explain what it means to be a solution to a system of linear equations in two variables.
14.15 Determine if a given ordered pair is a solution to a system of linear equations in two variables.
14.16 Solve by graphing systems of linear equations in two variables that have exactly one solution.
Unit 15 Sets (Optional)
General Outcome:
15.0 The student shall be able to identify & create sets, and perform basic operations on sets.
Specific Measurable Learning Outcomes:
Upon successful completion of this unit, the student shall be able to:
15.1 Define the terms “set” and “element.”
15.2 Create a set by listing its elements.
15.3
Identify elements and non-elements of a set using the notation ∈and
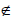 .
.
15.4 Define the term “empty (or null) set.”
15.5 Determine if a given set is finite or infinite.
15.6 Define the term “subset.”
15.7 Identify whether a set is or is not a subset of
another using the notation 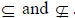
15.8 Determine the number of distinct subsets there are of a given set.
15.9 Define the terms “universal set (or universe),” “complement,” “union,” and “intersection.”
15.10 Determine the complement of any set by listing its elements.
15.11 Determine the union of any two sets by listing its elements.
15.12 Determine the intersection of any two sets by listing its elements.
15.13 Define the term “disjoint.”
15.14 Determine if any two sets are disjoint.


