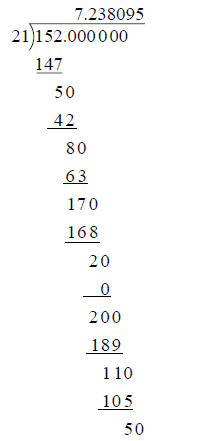Long Division
Long division is a collapsed version of the Euclidean Division algorithm. First, let’s remind ourselves what the Euclidean Algorithm is:
Euclidean Division Algorithm: If m and n
are integers and if n > 0, then there are unique integers q and r such
that m = nq + r and  |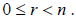
Another way to write this is to say that
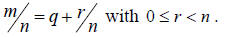
Let’s see how you use this to find the decimal
representation of any rational number. I will illustrate the process by finding
the decimal representation of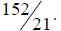 
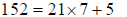
This first application gives us 7, the integer part of
this decimal. Each succeeding application uses 10 times the remainder from the
previous step. Here are the first 6 lines, which yield a quotient of 7.238095
and a remainder of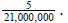
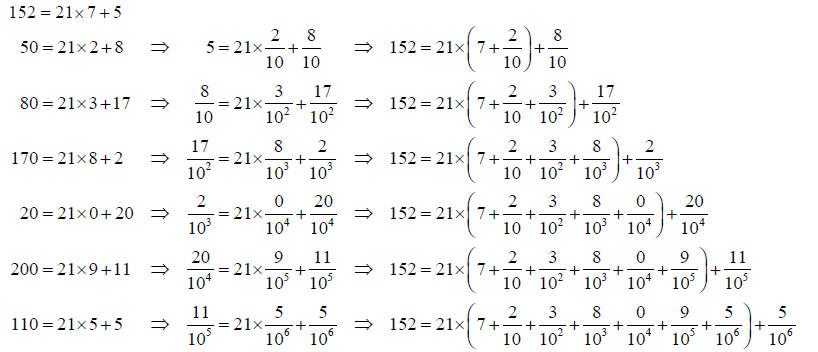
There are only 20 possible non-zero remainders when
dividing by 21 so the cycle of the quotients that begins 238095… must repeat
after at most 20 steps. In fact, since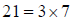 
, the
cycle repeats after 6 steps.
Now compare each line with the steps of the calculation from Long Division below. The final remainder 5 is equal to a remainder six steps earlier, so the cycle of quotients, 238095, will be repeated if the long division is continued.
