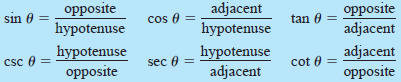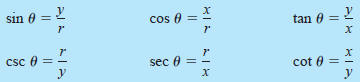Review of Trigonometric Functions
Standard position of an angle |
Angles and Degree Measure • Radian Measure • The
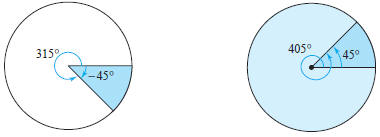
Trigonometric Functions • Evaluating Trigonometric Functions • Solving Trigonometric Equations • Graphs of Trigonometric Functions Angles and Degree Measure An angle has three parts: an initial ray, a terminal ray, and a vertex (the point of intersection of the two rays), as shown in Figure D.24. An angle is in standard position if its initial ray coincides with the positive x-axis and its vertex is at the origin. We assume that you are familiar with the degree measure of an angle. It is common practice to use θ (the Greek lowercase theta) to represent both an angle and its measure. Angles between 0° and 90° are acute, and angles between 90° and 180° are obtuse. Positive angles are measured counterclockwise, and negative angles are measured clockwise. For instance, Figure D.25 shows an angle whose measure is -45°.You cannot assign a measure to an angle by simply knowing where its initial and terminal rays are located. To measure an angle, you must also know how the terminal ray was revolved. For example, Figure D.25 shows that the angle measuring -45° has the same terminal ray as the angle measuring 315° Such angles are coterminal. In general, if θ is any angle, then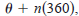 
n is a nonzero integeris coterminal with θ. An angle that is larger than 360° is one whose terminal ray has been revolved more than one full revolution counterclockwise, as shown in Figure D.26. You can form an angle whose measure is less than -360°by revolving a terminal ray more than one full revolution clockwise.
NOTE It is common to use the symbol θ to refer to
both an angle and its measure. For |
||||
.
|
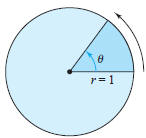
Radian Measure To assign a radian measure to an angle θ consider θ to be a central angle of a circle of radius 1, as shown in Figure D.27. The radian measure of θ is then defined to be the length of the arc of the sector. Because the circumference of a circle is 2 πr the circumference of a unit circle (of radius 1) is 2 π. This implies that the radian measure of an angle measuring 360° is 2 π .In other word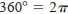s,  radians.Using radian measure for θ the length s of a circular arc of radius r is s = rθ , as shown in Figure D.28.
|
|||||||
|
You should know the conversions of the common angles shown in Figure
D.29. For other angles, use the fact that 180° is equal to π radians. |
|||||||
Radian and degree measure for several common angles
Figure D.29
| EXAMPLE 1 Conversions Between Degrees and Radians | |
 |
|
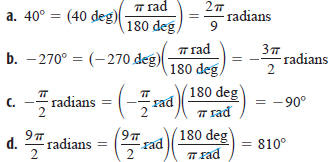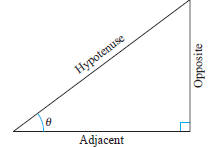
Sides of a right triangle
An angle in standard position |
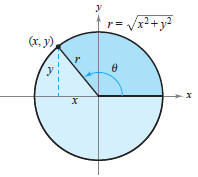
The Trigonometric Functions There are two common approaches to the study of trigonometry. In one, the trigonometric functions are defined as ratios of two sides of a right triangle. In the other, these functions are defined in terms of a point on the terminal side of an angle in standard position. We define the six trigonometric functions, sine, cosine, tangent, cotangent, secant, and cosecant (abbreviated as sin, cos, etc.), from both viewpoints. |
| Definition of the Six Trigonometric Functions Right triangle definitions, where 0< θ<π/2(see Figure D.30).
Circular function definitions, where θ is any angle (see Figure D.31).
|
|
|
The following trigonometric identities are direct consequences of the
definitions. (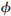 
is the Greek letter phi.) |
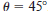