The Order of an Integer Modulo n

8.2. The order of an integer modulo n.

Definition. Suppose n > 1 and gcd(a, n) = 1. The order of a modulo n is the
smallest positive integer k such that a^k ≡ 1 (mod n).

Example: Consider the powers of 2 modulo 7:

so the order of 2 modulo 7 is 3.

Theorem (8.1). Let k be the order of a mod n. Then a^h ≡ 1 (mod n) iff k | h.

Proof: Use the division algorithm to write h = qk + r where 0 ≤ r < k. Now if
a^h ≡ 1 (mod n) then 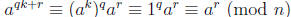. Then if r > 0 we have
a contradiction, because k is supposed to be the smallest positive integer such that
a^k ≡ 1 (mod n). So r = 0 and h = qk.

Now 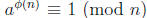by Euler’s Theorem. It follows that the order of a must
divide Ø(n). For example, Ø(7) = 6, and the order of 2 modulo 7 does divide 6.

Theorem (8.2). Let k be the order of a. Then 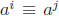(mod n) exactly when
i ≡ j (mod k).

The proof is just: 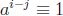(mod n) iff k | (i − j).

Corollary a, a², a³, . . . , a^k are incongruent modulo n.

Theorem. Suppose a has order k mod n. Let h be a positive integer. Then a^h
has order modulo n equal to k/ gcd(h, k).

Here’s an explanation rather than a complete proof. Suppose m is the order
of a^h, so (a^h)^m ≡ 1 (mod n), and m is the smallest such positive integer. So
a^mh ≡ 1 (mod n). But by the previous theorem, mh must be a multiple of k.
So we are looking for the smallest multiple of h that is a multiple of k. That
would have to be lcm(h, k). So mh = lcm(h, k). This is m = lcm(h, k)/h. Not
quite the right formula. But recall lcm(h, k) = hk/ gcd(h, k). It then follows that
m = k/ gcd(h, k).

Example. The order of 2 modulo 11 happens to be 10. Now the order of 2³
modulo 11 is also 10 since gcd(3, 10) = 1. But the order of 2⁴ ≡ 5 is 5 since
gcd(4, 10) = 2, and the order of 2⁵ ≡ 10 mod 11 is 2 since gcd(5, 10) = 5.

The order of an integer modulo n is of interest in general terms because it gives us
information about how exponentiation works in modular arithmetic. But here’s
an interesting little application that is not in Burton. It turns out that if a fraction
a/b has a repeating decimal, and gcd(b, 10) = 1, the length of the repeating block
happens to be the order of 10 modulo b.

Here’s an example: Find the decimal fraction for 1/7 using long division. You end
up doing the following calculations:

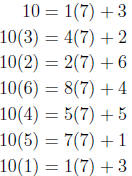
so it repeats, giving

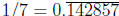
But compare the calculation of the order of 10 modulo 7:

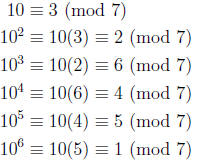
It’s the same calculation (except the quotients 1, 4, 2, 8, 5, 7 are hidden in the
congruences).

Theorem. Suppose gcd(b, 10) = 1. Then the fraction 1/b has a repeating decimal
block of length given by the order of 10 mod b.

Proof: Say 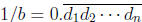, so the repeating block is n long. Now

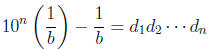(an integer).

So 10ⁿ − 1 is divisible by b. So 10ⁿ ≡ 1 (mod b). So n must be a multiple of the
order of 10 mod b. But suppose k is the order. Then 10^k ≡ 1 (mod b) implies
10^k − 1 = mb for some m, so

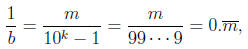
so the block length is no greater than k.

(A little more explanation: If you have a repeating decimal, say 0.345345345 · · · =
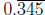, you can always write it as a fraction as 345/999.)

Here is some more detail on decimal expansions of rational numbers, from the
book An Introduction to the Theory of Numbers, 5^th Edition by the famous math-
ematicians G. H. Hardy and E. M. Wright. We will look at fractions of the form
a/b, where 0 < a/b < 1.

First, the decimal expansion for a/b terminates exactly when b = 2^m5ⁿ for some
m and n. For example, 17/160 = 0.10625 (160 = 2⁵ · 5). It turns out the decimal
expansion terminates after max{m, n} digits (in the example, 5 digits).

It turns out that if b = 2ⁿ5^mc, where gcd(c, 10) = 1, then there will be max{m, n}
non-recurring digits for a/b and then there will be a repeating block of length the
order of 10 mod c. Here’s an example: 125/88 = 1.420454545 · · · = 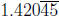. (Note
88 = 2³ · 11 and the order of 10 mod 11 is 2.)

8.2 Primitive roots

Suppose gcd(a, n) = 1. Then the order of a modulo n must divide Ø(n). If it
happens that the order of a equals Ø(n), so it’s the largest possible value for an
order, we call a a primitive root of n.

Examples: 2 is a primitive root of 11, since the order of 2 mod 11 is 10 and
Ø(11) = 10. But the order of 2 modulo 7 is 3, not Ø(7) = 6, so 2 is not a primitive
root of 7.

Theorem (8.4). If a is a primitive root of n then a, a², . . . , a^Ø(n) are incongruent
mod n. So they are congruent in some order to the positive integers less than n
that are relatively prime to n. So they form a “reduced set of residues” mod n.

Example: Look at 3 mod 10. The order of 3 mod 10 is 4. In fact, 3, 3², 3³, 3⁴ are
congruent to 3, 9, 7, 1 respectively, mod 10. And 1, 3, 7, 9 are the positive integers
less than 10 that are relatively prime to 10.

Primitive roots can be used to solve congruences involving exponentials. For
example, we can solve 7^x≡ 4 (mod 17). It happens that 3 is a primitive root of
17. So the order of 3 mod 17 is Ø (17) = 16. Now it turns out 7 ≡ 3¹¹ (mod 17)
and 4≡3¹² (mod 17). So the congruence 7^x≡ 4 (mod 17) becomes 3^11x ≡
3¹² (mod 17). But recall (mod n) iff i≡ j (mod k), where k is the order
of a mod n. So 11x ≡ 12 (mod 16). That happens to be solved by x ≡ 4 (mod 16).

Here’s another application of primitive roots: Recall if gcd(b, 10) = 1 then a/b has
a repeating decimal block of length the order of 10 mod b. If it happens that b
is prime and 10 is a primitive root of b , then the repeating block will have the
maximum-possible length of b − 1. But more interestingly, in that circumstance,
it turns out that if a ≠ 1 then the repeating block contains the same digits as the
repeating block for 1/b but given a “cyclic permutation.” For example,

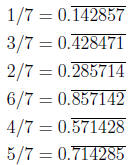
So primitive roots are interesting and useful. But unfortunately, not all integers
have them. For example, n = 8 does not have a primitive root. To verify this,
note Ø(8) = 4 so we are looking for a number relatively prime to 8 with order 4.
But only 1, 3, 5, 7 are relatively prime to 8; and the respective orders of these are
1, 2, 2, 2. The centerpiece of section 8.2 in Burton is the theorem:

Theorem(8.6). If p is prime and d | p−1, then there are exactly Ø(d) incongruent
integers with order d modulo p. In particular, there are Ø(p − 1) many primitive
roots.

So prime numbers have primitive roots. But:

Theorem (from section 8.3): If n = rs where r > 2 and s > 2 and gcd(r, s) = 1,
then n has no primitive root.

The proof of this is actually fairly simple. By multiplicativity of Ø we have Ø(n) =
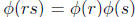. Now it happens that Ø(r) and Ø(s) are both even, since r and
s are bigger than 2 (see Theorem 7.4 in Burton). So by Euler’s Theorem, if a
is relatively prime to n we have 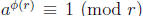. So .
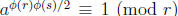Likewise a 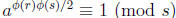. Therefore 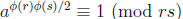. So the order
of a is less than .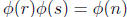

It turns out a number n > 1 has a primitive root exactly when n = 2, 4, p^k or 2p^k,
where p is an odd prime (Theorem 8.10 in Burton).

We now give a small example about how to find integers of a given order.

Example. Find all positive integers less than 41 with order 8 mod 41. Use the
fact that 6 is a primitive root of 41.

The idea is to look at powers of 6.

Theorem 8.6 says there are Ø(d) many integers with order d mod p if d | p − 1.
Here, d = 8 and p = 41. Of course, 8 | 40, so there are Ø(8) = 4 many integers of
order 8 mod 41. So we are looking for four powers of 6.

Recall if the order of a is k mod n then a^h has order k/ gcd(h, k) mod n. With
a = 6 and k = 40, the order will be 40/ gcd(h, 40). So all we need is h such that
this expression is 8. That is, we look for h such that gcd(h, 40) = 5. This leads to
h = 5, 15, 25, 35 only.

So our solution is 6⁵, 6¹⁵, 6²⁵, 6³⁵ ≡ 37, 3, 14, 38. These all have order 8 mod 41
and are the only numbers with that property.

We conclude with a little look at an interesting topic from section 8.4 of Burton:
the theory of indices.

Suppose n has a primitive root r. If gcd(a, n) = 1, define indra to be the smallest
positive number k such that a ≡ r^k (mod n). We call this the index of a relative
to r.

The point of this is as follows: One way of defining logarithms is to say that
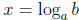provided a^x = b. For example, 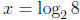solves 2^x = 8. So the index of
a relative to r resembles the logarithm of a base r. It turns out that indices obey
rules similar to those of logarithms:

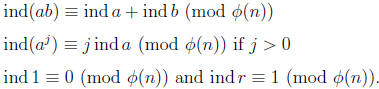
Now logarithms are used to solve exponential equations. Indices are used to solve
exponential congruences and the like.

Here’s an index table for 79, using the primitive root 3 of 79:

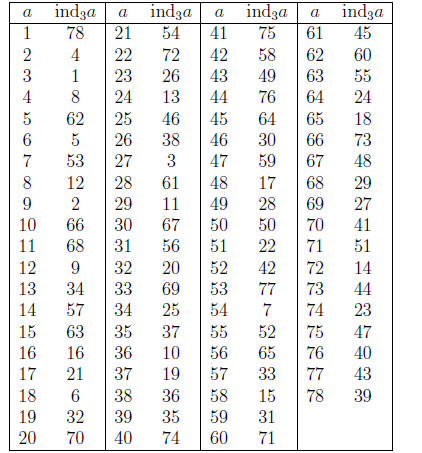
(For example, the table lists 4 with 8. That is, 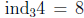; meaning that 3⁸ ≡
4 (mod 79), which is correct.)

Example: We can use this table to solve the congruence 5x⁷ ≡ 20 (mod 79). If
we take indices of both sides, and use the rules of indices (similar to the rules of
logarithms), we get



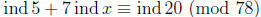
or



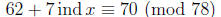
using the table. We solve this congruence for ind x as usual (think: 62 + 7y ≡
70 (mod 78)) to get ind x ≡ 68 (mod 78). Now use the table again, to find the
number with index 68. That turns out to be 11. So the solution of the original
congruence is x ≡11 (mod 78).

(Note, the modulus switches to 78 when we take indices because of Theorem 8.2:
(mod n) iff i ≡ j (mod k), assuming a has order k mod n.)