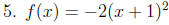The Square Root Property and Completing the Square
10.1 The Square Root Property and Completing the Square
An quadratic equation is written in standard form if it is
written as ax2+bx+c =
0 with (a ≠ 0).
If x2 = k then 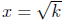 OR
OR
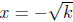 .
.
Examples: Solve each equation.
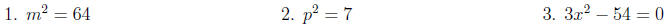
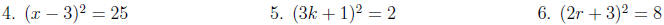
Steps to Completing the Square for an equation of the form
x2 + bx + c = 0:
1. But the terms with variables on one side and the constant on the other side.
2. Find
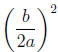 .
.
3. Add the square to both sides.
4. Factor the perfect square trinomial on the LHS.
5. Solve the equation using the methods discussed earlier.
Let's practice step 2:
Find the constant that should be added to get a perfect square trinomial.
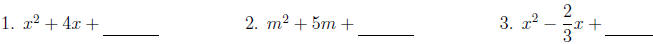
Examples: Solve each equation by completing the square:

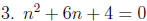
10.2 The Quadratic Formula
The solutions to ax2 + bx + c = 0(a ≠ 0) are given by
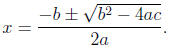
Tips:
1. Make sure you put the equation in standard form FIRST!
2. Be very careful when simplifying your answers.
Examples: Solve each equation using the quadratic formula.


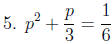
What is wrong with the following "solution" of 5x2 - 5x + 1 = 0?
10.3 Equations in Quadratic Form
Solve each equation:

Solve each problem:
1. In 1.75 hr, Ken rows his boat 5 mi upriver and comes back. The speed of the
current is 3 mph. How fast does Ken row?
2. Two chefs are preparing a banquet. One chef could
prepare the banquet in 2 hr
less time than the other. Together they complete the job in 5 hr. How long will
it
take the faster chef working alone?
Solve each equation. Be sure to check your answers.


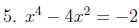
Summary of Ways to solve ax2 + bx + c = 0:
| Method | Advantages | Disadvantages |
| Factoring | This is usually the fastest method. |
Not all polynomials are factorable; some factorable polynomials are hard to factor. |
| Square root property |
This is the simplest method for solving equations of the form (ax + b)2 = c. |
Few equations are given in this form. |
| Completing the square |
This method can always be used, although most people prefer the quadratic formula. |
It requires more steps than other methods. |
| Quadratic Formula |
This method can always be used. |
It is more difficult than factoring because of the square root, although calculators can simplify its use. |
10.4 Formulas and Applications
Solve for the given variable:
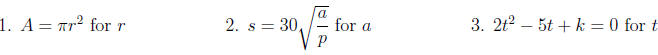
Word Problems:
Example 3 on pg. 592: Two cars left an intersection at the same time, one
heading
due north, the other due west. Some time later, they are exactly 100 mi apart.
The
car headed north had gone 20 mi further than the car headed west. How far had
each
car traveled?
#26 on pg. 596: A piece of sheet metal is 2 in. longer
than it is wide. A square
piece 3 in. on a side is cut from each corner. The sides are then turned up to
form an
uncovered box of volume 765 in.3. Find the dimensions of the original piece of
metal.
#5 on pg. 594: A ball is propelled vertically upward from
the ground. Its distance
in feet from the ground at t seconds is s(t) = -16t2 + 64t. At what times will
the
ball be 32 ft from the ground?
10.5 Graphs of Quadratic Functions
The graph of a quadratic equation is called a parabola.
Things to know about graphs of quadratic equations:
1. The graph of f(x) = a(x - h)2 + k, a ≠ 0 is a parabola with vertex (h, k)
and
vertical line x = h as axis.
2. The graph opens up if a is positive and down if a is negative.
3. The graph is winder than that of f(x) = x2 if 0 < lal < 1. The graph is
narrower
than that of f(x) = x2 if lal> 1.
Let's practice determining the vertex of a parabola and whether it opens upward
or
downward.
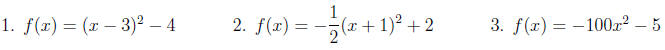
Graph the following. Give the vertex, axis, domain and range.