Density of Q in R

Theorem. (The Archimedean Property of R) The set N of natural numbers is unbounded
above in R.

Note: We will use the completeness axiom to prove this theorem. Although the Archimedean
property of R is a consequence of the completeness axiom, it is weaker than completeness.
Notice that N is also unbounded above in Q, even though Q is not complete. We also have an
example of an ordered field for which the Archmidean property does not hold! N is bounded
above in F, the field of rational polynomials!

Proof by contradiction. If N were bounded above in R, then by___
___N would have a___ . I.e., there exists m ∈
___such that m = ____. Since m is the ____,
___is not an upper bound for N. Thus there exists an 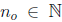  such that
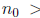
___. But then 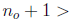___ , and since 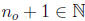, this contradicts___
___.

The Archimedean property is equivalent to many other statements about R and N.

12.10 Theorem. Each of the following is equivalent to the Archimedean property.

(a) For every z ∈ R, there exists an n ∈ N such that n > z.

(b) For every x > 0 and for every y ∈ R, there exists an n ∈ N such that nx > y.

(c) For every x > 0, there exists an n ∈ N such that .

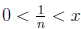The proof is given in the book. The idea is that (a) is the same as the Archimedean property
because (a) is essentially the statement that “For every z ∈ R, z is not an upper bound for
N.” Then, it is fairly easy to see why (b) and (c) follow.

Theorem (Q is dense in R). For every x, y ∈ R such that x < y, there exists a rational
number r such that x < r < y.

Notes: The idea of this proof is to find the numerator and denominator of the rational
number that will be between a given x and y. To do this, we first find a natural number
n for which n x and n y will be more than one unit apart (this will require the Archimedian
property!) Notice that the closer together x and y are, the bigger this n will need to be!
Picture (assuming x > 0):

Since nx and ny are far enough apart, we expect that there exists a natural number m in
between nx and ny. Finall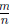y, will be the rational number in between x and y!

Proof. Let x, y ∈ R such that x < y be given. We will first prove the theorem in the
case x > 0. Since y − x > 0, ___∈ R. Then, by the Archimedean property, there
exists an n ∈ N such that n > ___. Therefore, ___< ny. Since we are in
the case x > 0, ___> 0 and there exists m ∈ N such that m − 1 ≤___< m (The
proof that such an m exists uses the well-ordering property of N; see Exercise 12.9.) Then,
ny > ___≥___. Thus nx < m < ny. It then follows that the rational number
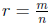satisfies x < r < y.

Now, in the case x ≤0, there exists k ∈ N such that k > |x|. Since k − |x| = k + x is
positive and k + x < k + y, the above argument proves that there is a rational number r
such that k + x < r < k + y. Then, letting r' = r − k, r' is a rational number such that
x < r' < y.

It is also true that for every x, y ∈ R such that x < y, there exists an irrational number
w such that x < w < y. Combining these facts, it follows that for every x, y ∈R such
that x < y there are in fact infinitely many rational numbers and infinitely many irrational
numbers in between x and y!