Solution of Linear Equations and Inequalities in One Variable
Definitions
1. Equation:
Need to apply same operations on BOTH sides!
2. Linear equation: an equation containing one variable and degree of terms at most 1.
Solving Linear Equations
Ex.1 (#10) Solve
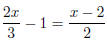for x.
| Steps | Solution |
| 1. If the equation contains
fractions, get rid of them by multiplying both sides by LCD of the fractions. 2. Remove any parentheses. 3. By adding/subtracting terms, get all terms containing variable that you are solving for on one side and all the other terms on the other side. 4. Divide both sides of the equation by the coefficient of the variable. 5. Check the solution by plugging it into the original equation. |
Fractional Equations: Equations with variables in a
denominator. Make sure to exclude the values
that make the denominator zero from the solution.
Ex.2 Solve for
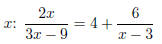
Linear Equations with Two (or More) Variables
• Treat the variable(s) for which you are not solving like numbers.
Ex.3 (#26) Solve for
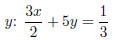
Inequalities
Solving an inequality = fining its solution "set"
• Multiplying/dividing both sides of an inequality by a negative number reverses
the direction of the
inequality symbol.
Ex.4 (#34) Solve the inequality and graph the solution:
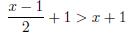
Stated Problems
From \Guideline for Solving Stated Problems" on page 65. of the textbook:
1. Begin by reading the problem carefully to determine what you are to find. Use
variables to represent
the quantities to be found.
2. Reread the problem and use your variables to translate given information into
algebraic expressions.
Often, drawing a figure is helpful.
3. Use the algebraic expressions and the problem statement to formulate an
equation (or equations).
4. Solve the equation(s).
5. Check the solution in the problem, not just in your equation(s). The answer
should satisfy the
conditions. Put a unit, if necessary.
Ex.5 (#48) The total price of a new car (including 6%
sales tax) is $21,041. How much of this is
tax?
Ex.6 (#52) Suppose a professor counts the final exam as
being equal to each of the other tests in her
course, and she will also change the lowest test score to match the final exam
score if the final exam score
is higher. If a student's four test scores are 83, 67, 52, and 90, what is the
lowest score the student can
earn on the final exam and still obtain at least an 80 average for the course?
3
Ex.7 (#58) Thirfty rents a compact car for $33 per day,
and Budget rents a similar car for $20 per day
plus an initial fee of $78. For how many days would it be cheaper to rent from
Budget? Graph the
solution.