Factor Those Tricky Trinomials
This lesson is designed for use in an 8th-grade,
Pre-Algebra, or Algebra classroom. The
lesson addresses factoring trinomials using algebra tiles, so it’s a hands-on
activity. It
should be taught with direct instruction and cooperative learning.
Standards:
8.PS.1 Use a variety of strategies to understand new
mathematical content and to develop
more efficient methods
8.CN.1 Understand and make connections among multiple representations of the
same
mathematical idea (Same as A.CN.1)
8.A.11 Factor a trinomial in the form ax^2 + bx + c; a=1 and c having no more
than three sets
of factors
A.A.20 Factor algebraic expressions completely, including trinomials with a lead
coefficient
of one (after factoring a GCF)
Objectives:
• Students will use manipulatives.
• Students will understand how to find the factors of trinomials using algebra
tiles.
• Students will use multiple representations to factor trinomials.
• Students will recognize the relationships between algebra tiles and
trinomials.
Materials:
• Algebra tiles for the students.
• Transparency tiles for the teacher, unless an ELMO is available.
• Paper and pencil.
Instructional Protocol:
• Be careful with terminology. There are multiple names for the individual types
of
algebra tiles. Find a consensus among the teachers in your school and stick with
one
set of names.
• Students need to be familiar with the concept of multiplying binomials with
the tiles
to create trinomials. Be sure it is covered before this lesson.
• Cooperative groups should be mixed so all students will benefit.
• Take time to oversee each group’s effort while they work. There is another
opportunity to help make corrections when a group presents their solution.
Factor Those Tricky Trinomials – Teacher Copy
A quick review of algebra tile basics would be helpful to begin the activity.
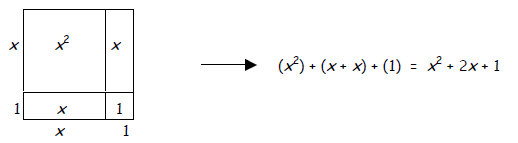
Given a trinomial, students must first use their algebra tiles to create the
appropriate
diagram. In this case, they should always have some type of rectangle.
A rectangle is a quadrilateral, prefix ‘quad.’ The trinomials we are working
with are
called quadratics, which also has the prefix ‘quad.’
Start with the trinomial x^2 + 3x + 2. Using the algebra tiles, the students
should obtain a
figure similar to the one shown below:

Next, look at the lengths that are represented by the diagram:
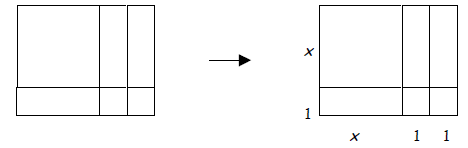
One side of the rectangle consists of two lengths: x and 1.
The total length of that side would then be the sum of the two lengths: x + 1.
The other side of the rectangle consists of three lengths: x, 1, and 1 again.
So the total length of the side is the sum of the parts: x + 2.
Now we have our two factors: (x + 1) and (x + 2).
To check, multiply the binomials using the FOIL method to see if we end up with
the same
trinomial.
FOIL: a pneumonic device used to make sure all parts of the binomials are
multiplied
together correctly and/or making sure the distribution is carried out properly.
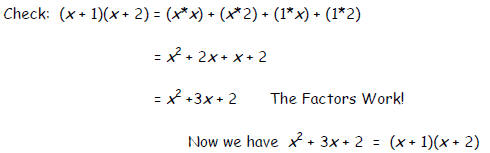
The activity then follows...
First and foremost, each group must have a cool team name. Each group of 2 – 3
students
will work together to factor trinomials using algebra tiles. After the correct
model has
been made, the students will then write out the factors and check their work.
The first team to complete the requirements above will use an overhead or an
ELMO to
share their results with the rest of the class.
If everything is done correctly, that team will earn points. Point values can
vary. Partial
points might also be an option if a team gets most of the answer correct. This
is an
excellent opportunity to award Red Pirates.
Here are some trinomials to get the game stared:
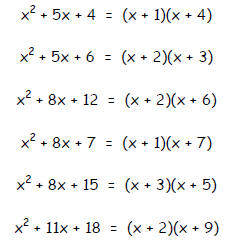
Factor Those Tricky Trinomials
Recall what each algebra tile represents:
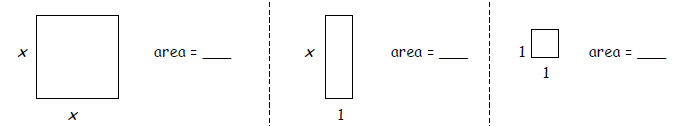
What do we know about the diagram below?(Fill in the missing lengths then give
the
binomials that describe each length.)

What method(s) did you use to find this trinomial?
______________________________
Now, use your algebra tiles to create a model of the trinomial x^2 + 3x + 2. In
the space
below, draw a diagram of the model.
Properly label the lengths in the diagram. Use these labels to find the binomial
factors:
( ____ + ____ ) and ( ____ + ____ )
Cool Team Name______________________________
Team Members_________________________________________________________
Make sure to draw a diagram for each model created with the algebra tiles.
Check each solution.