Precalculus with Graphing Calculators
TEXT: Precalculus, 3rd Edition, by Faires and DeFranza
NOTE: A graphing calculator is required for this course. The TI-86 should be
recommended for students who must purchase a new calculator for the course.
Students
who already own a graphing calculator should be encouraged to use the one they
have.
The main objective of this course is to prepare students to take MA 1713
Calculus I. The
course focuses on the specific pre-calculus concepts that are needed in Calculus
I in the
context and at the level of mathematical maturity normally encountered in
calculus.
Additionally, students will be taught the effective use of a graphing
calculator. The
terminology, level of exposition, and use of the calculator in the course should
closely match
what is commonly encountered in Calculus I. At least three graphing calculator
projects
that emphasize mathematical correctness and quality of presentation should be
assigned
and should reflect in the final grade. At least one of these should be a group
project.
Chapter 1, Sections 1.2 - 1.8: After completing Chapter 1, a student should:
- know the properties of inequality and the definition and properties of
absolute value.
- be able to find the solution set of linear and non-linear inequalities in one
variable
using analytical and graphical methods.
- know how to represent intervals graphically and using set and interval
notation.
- know the distance and midpoint formulas for two points in the coordinate
plane.
- know how to put the equation of a circle in standard form by completing the
square,
find the coordinates of the center and the radius, and graph the circle.
- know the difference in an equation and an identity.
- be able to determine the intercepts and symmetries of an equation in two
variables and
graph the equation without (or with a graphing calculator, as needed).
- be able to use the graph, window, trace, and evaluate operations on a graphing
calculator, as needed.
- know the definitions of function, domain, range, value of a function, odd
function and
even function.
- be able to evaluate functions analytically and by using their graphs.
- be able to find the domain of algebraic functions.
- know the definitions of linear and quadratic functions and how to find their
intercepts.
- be able to find the slope and y-intercept of a linear function, the critical
number of a
quadratic function, the extreme value of a quadratic function and to write
linear and
quadratic functions in standard form.
- be able to determine whether lines are parallel or perpendicular to a given
line.
- be able to write the equations of lines in point-slope, slope-intercept and
general form.s
| Section | Suggested minimum course Assignment |
| 1.2 1.3 1.4 1.5 1.6 1.7 1.8 |
p. 12:
1,2,5,7,9,12,16,19,27-35(odd),38,41,43,49,53,55,58,60,61 p. 19: 6,9,12,13,17,19,21,34,42,43,45,49,51,55,61,63 p. 25: 1-8,11,13,21,25,28,30,33,35,37,38-43 p. 32: 1bc,3bd,4,5,8,9,12 p. 46: 1acg,2h,3cde,4,5,7-15,17,20,21,23-31,37,41-51(odd), 52-55,57,61,68,69,71 p.58: 3,7,11,13,15,16,17bd,19,20,22,23-31(odd),35,37 p. 69: 3,7,11,13,20,21,23,28,29,31,33b,34,37,41 |
| 11 hours |
Chapter 2, Sections 2.1 – 2.5: After completing Chapter 2,
a student should:
- know the properties of, the domain and range, and be able to sketch the graphs
the absolute value function, the square root function, the cube root function,
and the greatest integer function.
- be able to graph more complicated functions from simpler functions by
understanding the algebra that produces horizontal or vertical shifts,
dilations,
or compressions in the graph.
- know the definitions o sum, difference, product, quotient and composition of
two functions and the inverse of a function.
- be able to find the domain of various combinations of algebraic functions.
- know the properties of inverse functions and how to make the graph of
of its inverse from the graph of a one-to-one function.
- understand the significance of the vertical and horizontal line tests as
applied to
a graph and whether or not the defining function is one-to-one.
| Section | Suggested minimum course assignment |
| 2.2 2.3 2.4 2.5 |
p. 86: 3,13,16,17ace,18a,19,22,25,27,30,33a-h p. 95: 3,6,7,11,14,18,19,21,23,25 p. 104: 1,3,5,8,10,13,16,17,20,21a,22,28,29,33,37 p. 114: 1-10,13,17,19,23,25,28,30,32,33,37,39 |
| 4 hours |
Chapter 3, Sections 3.1 – 3.6: After completing Chapter 3,
a student should :
- be able to define polynomial, rational and irrational function.
- be able to find intercepts and the behavior of the function as x → ∞ (or −∞ ).
- be able to use a graphing calculator to graph the polynomial and to find
critical
numbers and relative extreme values.
- know the Intermediate Value Theorem, the Division Algorithm, the Factor
Theorem, the Rational Zero Theorem, Descartes’ Rule of Signs and the
Fundamental Theorem of Algebra and how to apply them in solving polynomial
equations and finding the zeros of polynomial functions.
- be able to find the domain, intercepts, vertical, horizontal and slant
asymptotes
of rational functions and sketch their graphs with the help of a graphing
calculator.
- be able to find the domain and asymptotes, if they
exist, and sketch the graph
of irrational functions with the help of a graphing calculator.
- know how to perform complex arithmetic and determine complex roots of
polynomial equations.
| Section | Suggested minimum course assignment |
| 3.2 3.3. 3.4. 3.5. 3.6 |
p. 134: 1,3,4,5,7,11,13,15,23,2
6,33,34,35,39,41,43,47 p. 144 5,9,15,17,21,25,29,33,35,38,39 p. 157: 1-7,9,12,13,16,17,20,23,27,31,34,35,37,39,43 p. 163: 1,3,9,11,13,19,25,31 p. 172: 2,5,8,13,16,18,19,21,23,25,26,28,37,41,43,47,48,51,55: |
| 8 hours |
Chapter 4, Sections 4.1 – 4.9: After completing Chapter 3,
a student should:
- be able to define radian measure.
- be able to convert between degree and radian measure.
- know the definition of sine of t and cosine of t, where t is a real number and
that they are bounded, periodic functions.
- know that sine is an odd function and cosine is even.
- know the sine and cosine of the special angles (in radians) and the quadrantal
angles.
- be able to use reference angles to find the sine and cosine.
- be able to determine the amplitude, period and phase shift of sine and cosine
functions and sketch their graphs.
- know the definitions of the tangent, cotangent, secant and cosecant functions
in terms of sine and cosine, be able to determine their values for the
special and quadrantal angles, know their periods,aand be able to sketch their
graphs.
- know the Pythagorean identities and the sum, difference and double angle
identities for sine and cosine.
- know the half-angle identities and their derivation for sine and cosine,
i.e.,
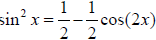 .
.
- be able to state and apply the trigonometric identities that commonly arise in
calculus and use them to solve problems.
- be able to solve applications using right-triangle trigonometry.
- be able to restrict the domain of trigonometric functions to produce
trigonometric functions that are invertible.
- be able to define the inverse trigonometric functions and give their domains,
ranges, and sketch their graphs.
- be able to work problems that involve inverse trigonometric functions.
- know the Law of Sines and the Law of Cosines and understand the
ambiguous case of the Law of Sines.
- be able to apply the Law of Sines and Law of Cosines to applications
involving oblique triangles.
- know how to add sine and cosine functions with the same argument to produce
a single sine (or cosine) function.
- know and be able to apply Heron’s formula and to find the area of a
triangle, given two sides and an included angle.
| Section | Suggested minimum course assignment |
| 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 |
p. 187: 1-9,
11-17(odd),18,21,24,25,29,31,33,34,35,38,40 p. 200: 1,2,3,5,6ab,7-53(odd) p. 210: 1-8,13,16,19,23-35(odd),36,37,40 p. 219: 1-9, 9-17(odd), 21,23,29,31,35,39,41 p. 231: 1-53(odd) p. 237: 1-17(odd) p. 246: 1-43(odd) p. 260: 1,5,9,13,15,17,19,22,23,25 |
| 12 days |
Chapter 5, Sections 5.1 – 5.4: After completing Chapter 5,
a student should:
- know the definition of e, how to approximate e, the definition of the natural
exponential function, its properties, and how to work problems involving
compound interest, and exponential growth or decay.
- know the definition of logarithm and natural logarithm and the properties of
logarithmic functions.
- be able to graph exponential and logarithmic functions and know the change of
base formulas for both exponential and logarithmic functions.
- be able to solve exponential and logarithmic equations in exact form and to
approximate solutions using a calculator.
| Section | Suggested minimum course assignment |
| 5.2 5.3 5.4 |
p. 282: 1,3,5,7,11,15,17,19,21,24,25,30,32a,38 p. 292: 1,5,9,13,17,21,25,29,32,33,37,39,53,57,61,65 p. 298: 1,5,7,9,13,17,19,22: |
| 3 days |
Other Pertinent Information for Instructors
1. The fall and spring semesters normally contain 45 class hours on a MWF
schedule; however, in the 2003-2004 academic year they contained 42 hours, only.
The summer
terms typically contain 42 hours. Sections 6.1 through 6.4 should be viewed as
optional.
The Course Outline suggests 38 hours of lecture. Three or four scheduled onehour
tests should be administered each semester in addition to a comprehensive
final examination.
2. Instructors are expected to teach their students how to use their calculators
wisely
and well.
3. Instructors are expected to use a graphing calculator
for the purpose of
enhancement and clarification of material in the course and for speed and
accuracy in calculation. They should teach students to give exact answers, when
possible, and to resort to calculator approximations at the appropriate stage in
their calculations.
4. Instructors should be aware of the symbolic manipulation capabilities of
certain
calculators (e.g. TI-89) and should exercise care in the construction of exams
so
that students using such calculators do not have an unfair advantage.
5. Calculators should be used on all scheduled tests and on the final
examination.
6. If time allows, students should be introduced to coordinate transformations
involving translations and rotations in the context of conic sections.
7. Instructors should take advantage of computer graded homework assignments
that
are available on the ILRN website of Brooks/Cole Publishing.
8. Instructors should assign at least three calculator projects during the
course of the
semester. The project reports should be graded for correctness, grammar,
spelling
and clarity of exposition. Graphs contained in the report should be neat, axes
should be labeled and tick marks should be labeled with appropriate units.


