The Buddy System and Its Implications

In our previous class, we adopted this principle:

Two sets have the same number of elements if and only if there exists a one-to-one
correspondence between them.

We agreed that this is a true statement for finite sets, and that we would accept it as the
defining characteristic for equality of size of infinite sets. Today you will use this idea as
you continue to explore sizes of infinite sets.

The original version of this packet was written by Prof. Michael Keynes. He likes to think
about one-to-one correspondence as a kind of buddy system. The rules of the buddy system
are simple. Two sets are the same size if we can buddy up their members so that:
1. Every member of one set gets a buddy from the other set
2. No member of either set has more than one buddy or no buddies.
These are the same conditions, expressed in different words, as those defining one-to-one
correspondences.

Using either interpretation, one-to-one correspondences or the buddy system, we can
determine if two sets have the same size without actually counting the elements of either set.
For example, we don’t have to count in our classroom to determine that there are the same
number of left eyes and right eyes because we can “buddy up” left and right eyes.

In working with the buddy system, it is often helpful to create a diagram showing how the
elements are paired. For example, in class we considered a way to pair up the numbers 1, 2,
3, … with the even numbers 2, 4, 6, … . The diagram for our pairing looks like



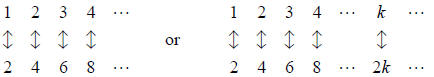
depending on whether or not we want to include a variable to define the general rule. In the
activities in this packet, these will be referred to as arrow diagrams. Also, we will use the
symbol to stand for the set of natural numbers, {1, 2, 3, … }.

1. Let’s compare the natural numbers, , with a new set of numbers where we have all the
natural numbers except 1. We’ll call this the “one-less natural numbers” and
abbreviate them as – {1}. Consider the elements of the first set to be colored red, and
those of the second blue. Set up a buddy system between red and blue – {1} by
drawing an appropriate arrow diagram. Then answer the questions on the next page.

a. In your buddy system, what is paired with red 73? With red 34827?

b. What is paired with blue 42? Blue 1007?

c. Does every red number have a blue buddy? Using a variable, if k is any red
number, what is the blue buddy?

d. Does every blue number have a red buddy? Using a variable, if n is any blue
number, what is the red buddy?

e. Does any red or blue number have more than one buddy? Why or why not?

f. Based on your buddy system, compare the sizes of red and blue – {1}. Does
one set have more elements, or are the two sets the same size? Explain.

2. Our Scottish skeptical friend, Rodney MacDoubt, says he doesn’t believe they are the
same size because he can set up a buddy system that doesn’t work. To explain what his
buddy system is, he uses the following arrow diagram.

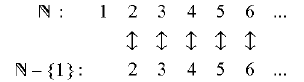
Using this buddy system, the red 1 (from ) doesn’t get a buddy, so it doesn’t work.
Does this mean that and – {1} aren’t the same size?

Can you reconcile this with what you found in the previous problem?

Unexpected Implications

The last question on the preceding page points out an important technicality in our concept
of equal size for infinite set: when we say that a one-to-one correspondence exists, that
doesn’t mean that every possible correspondence will be one-to-one. It just means there has
to be at least one. This has a surprising implication when dealing with infinite sets. It is
possible to have one pairing that uses all the elements of one set and leaves some elements
of the other unpaired, and at the same time there can be another pairing that uses all the
elements of the second set while leaving some of the elements of the first unpaired. And for
these same two sets there may be yet another pairing that establishes a valid one-to-one
correspondence.

1. Consider two copies of , one red and one blue. There is an obvious one-to-one
correspondence between them. What is it? (Tell which blue number is paired to
each red number, and vice versa).

2. Make up a pairing so that each red number is paired with one blue number, and no
two red numbers share the same blue number, but so that some blue number is left
unpaired. Show your pairing with an arrow diagram.

3. Similarly, make up a pairing so that each blue number is paired with a red number,
and no two blue numbers share the same red number, but this time with one red
number left unpaired. Again, show your pairing with an arrow diagram.

4. Do you think this situation can occur for two finite sets? That is, could there be two
finite sets for which one way of pairing them up uses all the elements of the first set
but leaves one or more elements of the second unpaired, while another way of
pairing them reverses the situation, and yet another way of pairing them uses all the
elements of each set?

One important issue to be aware of is that infinity (often labeled ∞), is not a number in the
usual sense. It is possible to extend our number system to incorporate ∞, but it doesn’t obey
the familiar rules. For example, your earlier work shows that you can add one element to
an infinite set and find that the resulting set has the same size as the one you started with.
For example, if the first set is – 1 = {2, 3, 4, … } and we add the single element 1, the
resulting set is = {1, 2, 3, 4, … }. And you know that – 1 and have the same size
because you found a way to buddy them up. That seems to say that ∞ + 1 = ∞. This is
contrary to what you would expect for arithmetic, but lends support to those in the class who
argued that all sizes of infinity must be the same. However, let us not jump to any hasty
conclusions. We have just begun to explore the implications of the buddy system concept.
Our explorations continue …

1. Set up a buddy system for and the whole numbers, {0, 1, 2, 3, 4, …}.

2. On page one there is an arrow diagram for a buddy system pairing the natural numbers
with the even natural numbers (we can abbreviate that as 2). Make a copy of that
below. Next find a buddy system between 2 and the odd numbers {1, 3, 5, 7, …}, and
make an arrow diagram for that. By combining the two arrow diagrams you can create a
buddy system between and the odd numbers. Explain how.

3. The integers include all positive and negative natural numbers, as well as 0 (which, by
the way, is officially neither positive nor negative). We abbreviate this set as 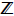(The
letter “Z” was chosen because the word for number in German is “Zahlen.” Germans
were very influential in the development of Mathematics.) Find a buddy system for the
and 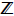. (This can be tricky.)

Hotel Infinity

It’s the stranded traveler’s fantasy: The Hotel Infinity has as many rooms as there are
natural numbers. The room numbers are 1, 2, 3, 4, 5, etc… You can see why stranded
travelers love this hotel.

1. Suppose you come to the hotel late one night and the sign says: “No Vacancy.” All the
rooms are occupied. The night manager assures you there is a way to provide you with a
private room without evicting another guest or forcing anyone else to share a room,
although it might be necessary to shift the guests around a bit. Explain how this can be
done.

2. This problem uses the same reasoning as one of the buddy systems you created between
and another set on a previous page in this packet. Which buddy system is it and why
is the reasoning the same?

3. Here is a variant on question number 1: This time you and two of your friends come to a
fully occupied Hotel Infinity. How could you all get private rooms?

4. Motel Infinity is a cheaper version of Hotel Infinity. They have an infinite number of
rooms as well, it’s just that they have no HBO and aren’t as clean. Suppose one night
they are fully occupied. They discover they not only have an infinite number of guests,
but an infinite number of bed bugs. They are forced to fumigate and all of their guests
need to find other accommodations. They all go across the street to Hotel Infinity,
which is also fully occupied. Can the night manager find a way to give private rooms to
all the current guests and new guests from Motel Infinity? If so, how would he do it
(and what question from an earlier page employs similar reasoning)? If not, why is it
impossible?

Whole Numbers and Fractions

So far, it seems that all infinite sets of numbers seem to be the same size. Let’s put this to
the test. The set of all rational number (all fractions, both positive and negative) is denoted
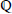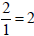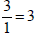as . This clearly includes all natural numbers (because, for example, and ), but
also includes many other numbers such as 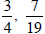, and .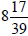
For right now, let’s just deal
with the positive rational numbers, which we’ll call 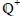. Is there a way to set up a buddy
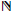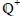system between and ?. If so, what is it? If not, why do you know it can’t be done?
Here’s a way to start: We can put all of the positive fractions in an infinite table like so:

This lists every rational number many times, in fact an infinite number of times, because all
of the different fractional forms are included. For example, the table includes 1/1 and 2/2
and 3/3, etc, all of which equal the rational number 1. Your task: find a buddy system
between the entries in the table and the natural numbers .