Fractions of Whole Numbers

Consider the following problem.
 Suppose that a class of twenty students took
a math test and only 5 students made a passing grade. To describe such a
situation one will say that one fourth of the class passed and three-fourth
failed. The class is considered as a unit. We "break" this unit into four
groups each consisting of five
students. One of the group consists of those
students who passed the test and the other three consist of those students
who failed the test. Considerations like these lead to the introduction of
fractions.
The word fraction comes from the Latin word fractius which means "to
break". When an object is divided into an equal number of parts then each
part is called a fraction.
There are different ways of writing a fraction. For example, two fifths of an
object can be written as
•a common fraction:2/5
•a decimal 0.4
•a percentage 40%
We will learn about percentages and decimals later.

Now, let us have a closer look at the common fraction : a/b .
•The number a is called the numerator and represents the number of parts
in consideration.
•The number b is called the denominator and represents how many equal
parts in the unit. Keep in mind that this number can never be zero since
division by zero is undefined.

Example 18.1
Show that any whole number is a fraction.

Solution.
If a is a whole number then we can write a as the fraction a/1 .
 

Different Types of Fractions
There are 3 different types of fractions.
 

•Proper Fractions
Proper fractions have the numerator part smaller than the denominator part, for example 2/5 .
 

•Improper Fractions
Improper fractions have the numerator part greater or equal to the denomi-
nator part, for example 7/6 .

•Mixed Fractions
Mixed fractions have a whole number plus a fraction, for example,

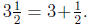
Pictorial Representation of a Fraction
Several physical and pictorial representations are useful in the elementary
school classroom to illustrate fraction concepts. We consider four different
pictorial representations of a fraction.

•Colored Regions
A shape is chosen to represent the unit and is then subdivided into equal
parts. A fraction is visualized by coloring some of the parts as shown in
Figure 18.1.

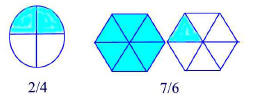
Figure 18.1

•The Set Model
Figure 18.2 shows a set of 7 apples that contains a subset of 3 that are wormy.
Therefore, we would say that 3/7 of the apples are wormy.

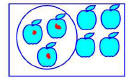
Figure 18.2

•Fraction Strips
Here the unit is defined by a rectangular strip. A fraction a/b is modeled by
shading a parts of the b equally sized subrectangles. Sample fraction strips
are shown in Figure 18.3.

Figure 18.3

•The Number-Line Model
A fraction such as 5/4 is assigned to a point along the number line by sub-
dividing the interval [0, 1] into four equal parts, and then counting o 5 of
these lengths to the right of 0 as shown in Figure 18.4.

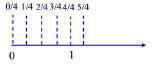
Figure 18.4

Practice Problems

Problem 18.1
Explain how to complete each diagram so that it shows 3/10 .
 

Problem 18.2
A child shows 4/5 as

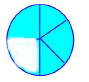
What is wrong with the diagram?

Problem 18.3
What fraction is represented by the shaded parts?

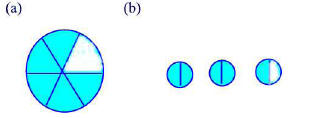
Problem 18.4
Depict the fraction 4/6 with the following models.
(a) Colored region model
(b) Set model
(c) Fraction strip model
(d) Number-line model.

Problem 18.5
Express the following quantities by a fraction placed in the blank space.
(a) 20 minutes is ___ of an hour.
(b) 30 seconds is ___ of a minute.
(c) 5 days is ___ of a week.
(d) 25 years is ___ of a century.
(e) A quarter is ___ of a dollar.
(f) 3 eggs is ___ of a dozen.

Problem 18.6
Three fifths of a class of 25 students are girls. How many are girls?

Problem 18.7
The Independent party received one-eleventh of the 6,186,279 votes cast.
How many votes did the party receive?