Home
Syllabus for Intermediate Algebra
MATH 001 Introductory Algebra
Math 80 - Test 4 Review
The Order of an Integer Modulo n
Elementary Algebra II homework
Syllabus for Introduction to Algebra, Elementary Algebra and Intermediate Algebra
Polynomial Functions
factoring_trinomials
Multiplying Polynomials
Solution of Linear Equations and Inequalities in One Variable
Elementary and Intermediate Algebra
Course Syllabus for Contemporary Math
Long Division Face
Math 107 Exam 1 Practice
Arithmetic Test
Long Division
Applied Linear Algebra
Course Syllabus for Intermediate Algebra
Things to Know
Elementary Linear Algebra
Lines and the Cartesian Plane
Quadratic Equations
Images and Inverse Image of a Set
COURSE OUTLINE FOR PRECALCULUS
Fractions
Pre-Calculus I
factorthosetrickytrinomials
Fractions of Whole Numbers
SYLLABUS FOR COLLEGE ALGEBRA
calculus_with_analytic_geometry-mkiqddbawj
Graphing Calculator Guide - Regression
Matrices And Matrix Operations
Algebra in Middle School Mathematics
TECHNICAL MATH I COURSE INFORMATION
Multiplying Polynomials
Pre-Algebra Exam 1 Solutions
MATRIX ALGEBRA:DETERMINANTS,INVERSES,EIGENVALUES
Introduction to Number Theory Review Sheet for Exam #2
Quiz of quadratic function
MATH 0098 Intermediate Algebra Syllabus
The Applied and Computational Mathematics (ACM) Program
Review for Math 3345 Test #1
Investigating Liner Equations Using Graphing Calculator
Exponents and Polynomials Worksheet
Equations Containing Rational Expressions
Precalculus with Graphing Calculators
Math 327A Exercise 2
Finding Common Denominators
MATH 101 Basic Mathematics
Descriptions of Mathematics
Syllabus for Elementary Algebra
Finding Solutions of Polynomial Equations
Intersections of Tangent Lines of Exponential Functions
Exponential and Logarithmic Equations
Elementary Algebra
COURSE SYLLABUS FOR INTERMEDIATE ALGEBRA WITH APPLICATIONS
Learning Standards for Mathematics
Numerical Linear Algebra
Review of Polynomials and Radical Expressions
systems of linear equations
MATHEMATICS Course Descriptions
Integrals of Rational Functions
Course Syllabus for College Algebra
INTEGRATED ARITHMETIC AND ALGEBRA
Fundamental Mathematics IV
Practice Exit Exam 2 for MATH 0024
Elementary Algebra Review
Radical Notation and Rational Exponents
Factoring
Graphs of Equations and Functions
Retrieving the Green's function
INTEGRATION MATH 21 B
FINITE MATHEMATICS
The Square Root Property and Completing the Square
Counting Money at Gary's Grocery Market
INTERMEDIATE ALGEBRA COURSE SCHEDULE
Introduction to Control Systems
Test I Guide
The Vertex and Quadratic Formula
Rational Exponents
Properties of Geometric Shapes
Test Description for FRACTIONS
Course Syllabus for College Algebra
Section 1.2: Straight lines
Solutions to Math Complex Problems
PRE-CALCULUS ALGEBRA
Algebra
A Parent Guide to Grade 4 Mathematics
The Buddy System and Its Implications
Multiplying Polynomials
Graphing Quadratic Equations
COURSE OUTLINE FOR INTERMEDIATE ALGEBRA
Introduction to Linear Algebra
Density of Q in R
Fractions
Engineering Mathematics
Math Department Meeting Notes
Model Academic Standards for Mathematics
Review of Trigonometric Functions
Math 117 SCHEDULE

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Quiz of quadratic function

1) A quadratic function is given. Express the quadratic function in standard
form. Find the vertex and its intercepts. Sketch its graph, clearly indicating
the vertex and the intercepts.

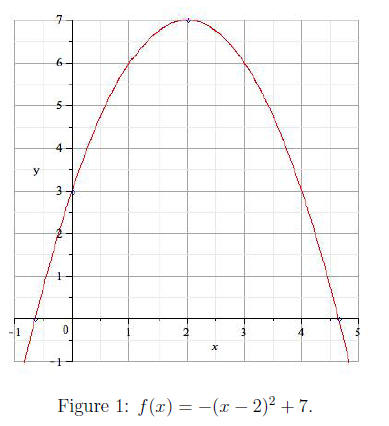
f(x) = −x^2 + 4x + 3

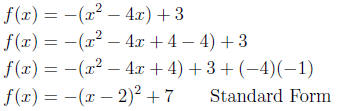
The vertex is (2, 7), the y-intercept is 3, and the x-intercepts are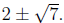

2) Find two numbers whose sum is 17 and whose product is as large as
possible. Write down the quadratic function that needs to be maximized,
clearly indicating what all the variables mean. Complete the square or use
some appropriate formula to obtain these two numbers.

Let x and y be the two numbers with sum 17 (x + y = 17) and let P be
the product, that is, P = xy. Now,

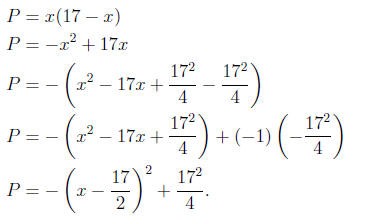
So the maximum occurs when x = 17/2 . This means that the two numbers are
both equal to 17/2 (x = 17/2 and y = 17 − x = 17/2).