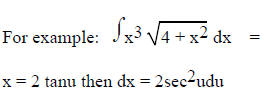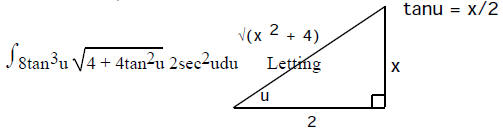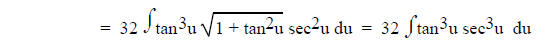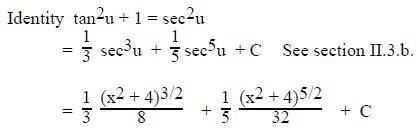INTEGRATION MATH 21 B
The first step in all integration problems is to determine
which type of problem it is . . .algebra (no
exponentials (e's), logs or trig), trig or mixture (some combination of algebra,
exponentials (e's), logs and trig).
The following outline suggests an orderly approach to deciding which integration
technique to use.
I. Algebra
A. Can you make it an exponent problem? [Any necessary quantities in parentheses
are raised to
a whole number power.]
By an exponent problem, I mean any expression which may be
written as the sums and/or differences of
terms of the form axn where a and n are constants.
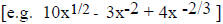
For example: (2x + 3)2 = 4x2 + 12x + 9,
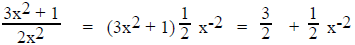
are each written in the desired form. Note that any terms
in parentheses are raised to a whole number power.
These functions may now be integrated by the power rule.
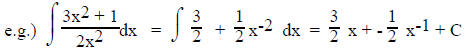
Integrands like
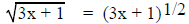 and
and
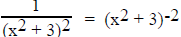 require parentheses with powers that
require parentheses with powers that
are not whole numbers and therefore cannot be written as exponent problems.
B. Does the derivative of one part = the other part?
[Substitution - The degree of one part is one
more than the degree of the other part. Let u = the part with the higher
degree.]
Taking the derivative of an expression lowers the degree
of the expression by one. Therefore, if the derivative
of one part is to equal the other part, it is clear that the powers must differ
by one.
For example the degree of 4x2 + 2x - 13 and that of 8x +
2 differ by one (2 and 1 respectively) so in this case
try letting u = 4x2 + 2x - 13, the one with the larger power. Since du = (8x +
2)dx we are in luck.
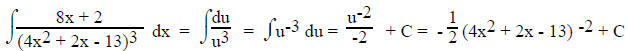
If du can be obtained by multiplying the "other part," by
a constant, this still works. In this case, multiply the
other part by the necessary constant and multiply the integral by the reciprocal
of the constant. This results in
du appearing in the integrand.
For example:
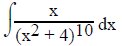 Note that the degree of x and x2 + 4, we can choose to ignore the exponent 10
Note that the degree of x and x2 + 4, we can choose to ignore the exponent 10
for now, differ by one. Let u = x2 + 4 , then du = 2xdx which is not exactly in
the problem. Note that
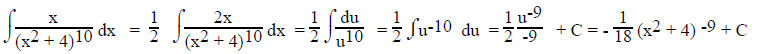
We want du = 2xdx to appear in the problem so we
multiplied x by 2 and the integral by the reciprocal of 2.
Sometimes the powers differ by one but this method doesn't work. Given
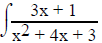 dx , letting
dx , letting
u = x2 + 4x + 3 seems appropriate but du = 2x + 4 and
there is not a constant that when multiplied by 3x + 1
will give us du. So, proceed to the next question.
C. Tricks
1. Long division. The degree of the numerator is ≥ the
degree of the denominator.
Consider
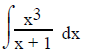 .
The degree of the numerator (3) > the degree of the denominator (1).
.
The degree of the numerator (3) > the degree of the denominator (1).
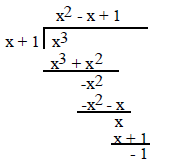
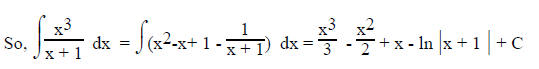
2. Partial Fractions. The denominator factors.
Since we got this far in the questions the degree of the
numerator is less then the degree of the denominator. If
the denominator factors, the integrand can be rewritten using partial fraction
decomposition. For example:
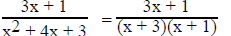 which can be written as
which can be written as
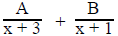 as follows:
as follows:
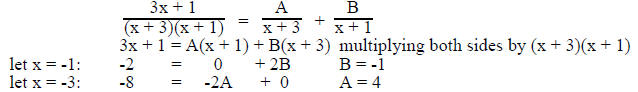
Now substituting A & B we have,
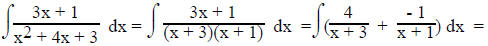

3. Completing the square.
The denominator is usually a quadratic and can be written in the form (x + a)2 + b
For example:
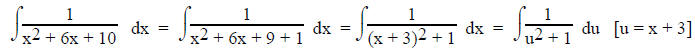
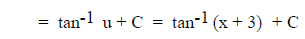
4. Trig substitution.
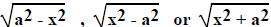
appear in the integrand. Let x =  a sinu, x = a secu or x = a tanu
a sinu, x = a secu or x = a tanu
respectively.