Investigating Liner Equations Using Graphing Calculator

Activity 2
Graphing Lines of the Form y = mx + b

Objective: In this lesson you will see how the constant b affects the line graph.

1. Use a graphing calculator to graph each equation and complete the following
chart. An example is solved for you.

Equation	Value of m	Value of b	Sketch	y-intercept	x-intercept
y = x – 3	1	-3		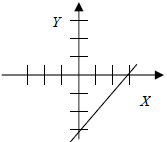(0,-3)	(3,0)
y = x + 4
y = x + 5.5
y = 2x – 5
y = 2x + 4.8
y = 3x – 2
y = -3x + 7
y = -3x

2. Use the results to answer the following questions.
a. If b has a positive value, then the y-intercept is (above, below) the x-axis. Circle one answer.
b. If b has a negative value, then the y-intercept is (above, below) the x-axis. Circle one answer.
c. What is the y-intercept of the equation y = 2x + 4? _________________________
d. What is the y-intercept of the equation y = mx + b? ________________________

3. Answer the following questions about the first three entries in Exercise 1.
a. What is the same about all three graphs? ________________________________
b. These lines never intersect so we say they are ___________________________
c. What is the relationship between b and the x-intercept in these equations?
____________________________________________________________________
d. What are the x- and y-intercepts of y = x – 5? ____________________________
e. How does changing the value of b affect graphs of the form y = x + b? _________
____________________________________________________________________

4. Describe and compare the graphs of y = 3x – 1 and y = 3x + 2. (Use a graphing
calculator to help you see the graphs.) __________________________________
____________________________________________________________________
____________________________________________________________________

5. Write an equation whose graph is a horizontal line. ________________________

6. Write an equation whose graph is a horizontal line through (0, 2.5). ____________

7. Write an equation whose graph is a line parallel to and between the graphs of
y = 3x + 2 and y = 3x + 4.5 ____________________________________________

8. Write and equation whose graph is a line parallel to the graph of y = -3x + 1, but with
y-intercept (0,-5). ____________________________________________________

Activity 3
Graphing Lines

Objective: In this lesson you will see how to graph equations that are not in the
slope-intercept form y = mx + b.

Solve each equation for y then write the equation in slope-intercept form. Find the
slope, and x- and y-intercepts, and graph the line. An example is solved.

Equation	Equation in slope-intercept form	sketch
2x + y – 3 = 0 Solve for y:	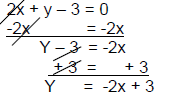Y = -2x + 3 Slope = -2 y-intercept =(0,3) x-intercept = (1.5,0)
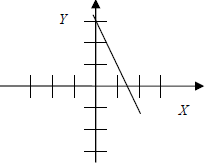Y + 3x = 4
Y – 3.5 = 2x
5x – y = 15
-1x = 4 + y
2y + 5x – 7 = 0
Challenge: Write your own problem below. Follow the directions above to solve and graph the line.

Activity 4
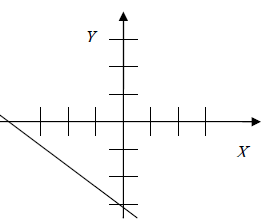
Find That Equation

Objective: In this lesson you will see how to find the equation of a line by looking
at its graph.

Examine each graph below and predict its equation. Then use the graphing calculator
to test your prediction. The first problem is solved for you.

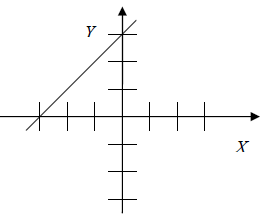	Reasoning: The y-intercept is (0, 3). ----->" b = 3 The slope is positive and equals 1. ---->" m = 1 The slope-intercept form ----->" y = mx + b Substitute the values of m and b. y = 1x +3 Equation: y = x + 3
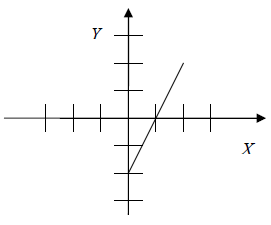
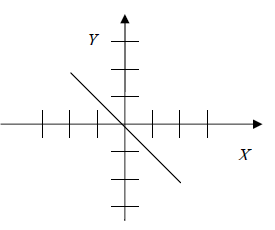
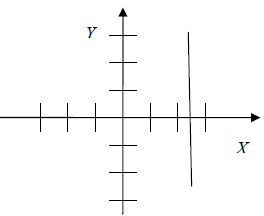
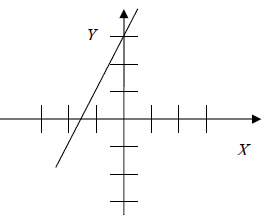
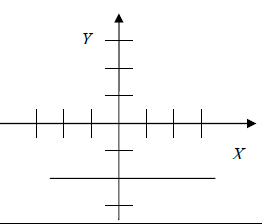