The Vertex and Quadratic Formula

Here are a few hints and solutions to the most popular questions in the math study center today. Make sure to thank
your classmates for asking good questions. I hope this helps get you through this assignment.
Remember that this assignment is very important and will be emphasized on Exam 2!

Worksheet 13. The Vertex and Quadratic Formulas

1. PROBLEM 22(b). How much time has gone by from the time Car F reaches 2 miles to the time the Car F reaches
7 miles?

•First find the times in question. That is, solve F(t) = 2 and separately solve F(t) = 7 (taking the first time
solutions for each). Find the difference between these times.

2. PROBLEM 22(c). Car G has a LINEAR distance vs. time graph. Find the formula for G(t).

•When you see the word LINEAR (or the words constant rate), you should immediately recognize that you
are talking about the equation for a line. Namely y = mx + b (or G(t) = mt + b using the variables in this
case) and your job is to find m and b.

•To find m and b you need to find two points.
- When t = 0, Car F is a 0 miles and Car G is 5 miles ahead of F. So for the G line one point is (0,5).
- When t = 9, Car F is at 16.875 miles and Car F is passing by Car G so they are at the same distance. So
for the G line another points is (9,16.875).
- Now find the slope and the y-intercept and you will have the equation for the line.

3. PROBLEM 23(f). Find when the water level for Vat A is increasing and the difference B(t)-A(t) is also increasing.

•THIS PROBLEM HAS TO DO WITH THE VERTEX FORMULA.
•Looking at the parabola graph for A(t), we see that A(t) goes down (DECREASES) from t = 0 to the vertex
at t = 4 (you found this in part (a)). AND A(t) goes up (INCREASES) from after t = 4.
•Now we need the formula for B(t) - A(t) before we can answer any questions about it. In part (e), you found
this formula and discovered that the vertex is at t = 4.25. Since the parabola for B(t)-A(t) opens downward,
it increases from t = 0 to t = 4.25 and decreases after t = 4.25.
•The only times that they are both increasing is between t = 4 and t = 4.25.

4. PROBLEM 26(e). At what times are the two cars 5 feet apart?

•The average trip speed for the first car is 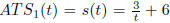. Since ATS(t) = D(t)/t , we also know that
D(t) = t * ATS(t).
Thus, to get distance we must multiply average trip speed by t. Hence, the distance formula for the first car is

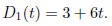
•The average trip speed for the second car is 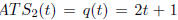. Hence the distance formula for the
second car is

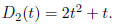
•"Car 1 is 5 feet ahead of Car 2" when

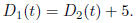
You can solve this and use the quadratic formula to get two answers. "Car 2 is 5 feet ahead of Car 1" when

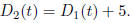
You can solve this and use the quadratic formula to get answers. It turns out that you only get three answers
total.

5. PROBLEM 27(c)(e). Find the graph for q(x) and the largest value of q(x) from x = 1 to x = 5.

•The formula for q(x) is

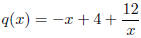
This is not a line or a quadratic so that only way that we can understand what is going on is by plugging in

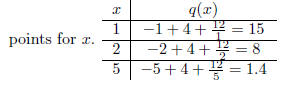
•Plotting this points we see that only the third graph makes sense.
•To find the largest formula we CANNOT use the vertex formula. But from the graph we can clearly see that
the largest value is at x = 1 and the value is 15.

Worksheet 14. Revenue and Profit as Rectangles

1. Algebra hints for PROBLEM 18

•To solve 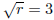you must square both sides to get r = 9.
•To solve 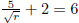. First simplify and get rid of your fractions. That is,

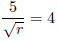(subracting 2 from both sides)

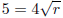(multiplying both sides by the denominator).

So 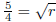(now you can square both sides).

•In general, if you have a fraction in an equation, multiply both sides by the denominator to get rid of all
fractions (this usually makes it much easier to solve the problem).