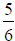Finding Common Denominators
Learning how to find common denominators is an essential
skill for every math student. This
handout will provide a step-by-step approach to finding common denominators.
Before learning how to find common denominators, it is important to understand
least common
multiples and how they work.
Least Common Multiple - Multiples of a number are the products of the
number and the
numbers 1, 2, 3, 4, 5 . . . . In other words,
and so on.
The least common multiple (LCM) is the smallest common
multiple that two or more numbers
share. For instance, the least common multiple of the numbers 4 and 6 is 12.
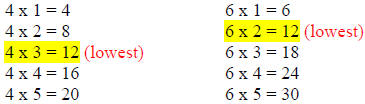
Least common multiples are necessary when finding common
denominators because they are
needed in order to find the lowest common denominator (LCD) of a fraction. The
LCD is
needed when operations such as addition and subtraction are being performed and
the fractions
contain denominators that are not the same.
To find the least common denominator
To add fractions with unlike denominators, first the fractions must be rewritten
as equivalent
fractions with a common denominator. The common denominator is found by
identifying the
least common multiple of the denominators of the fractions. The following is a
step-by-step
explanation of how to do this.
Add: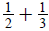
Step 1: Create a multiples table for the denominators.
In the exercise, the denominators for the fractions are 2 and 3. In order to
find the lowest
common denominator for the two fractions, the least common multiple of the two
numbers must
be found.
The least common multiple for 2 and 3 is 6. When
working with fractions, the least common
multiple is often called the least common denominator. Both terms refer to the
same thing.
Step 2: Rewrite the original fractions as equivalent fractions with a common
denominator.
• To rewrite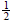 
as an equivalent fraction with
a denominator of 6, begin by placing the 6 in the denominator slot
of the equivalent fraction.
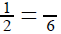
• Then, using the multiples table, identify what number,
when multiplied by 2, gives an answer of 6. In this case,
2 x 3 = 6; therefore, the number is 3.
• To complete the equivalent fraction, multiply the 3 by the numerator of the
original fraction ( 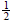). Therefore,
the equivalent fraction of 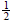is
.
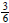• Another way to look at this: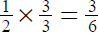
• Repeat the process to obtain the equivalent fraction for
.
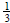Step 3: Now add the numerators of the equivalent fractions and retain the
common
denominator.
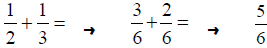
The correct answer is 