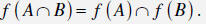Images and Inverse Image of a Set
| Purpose of Section: To introduce the concept of
the image and inverse image of a set. We show that unions of sets are preserved under a mapping whereas only one-to-one functions are preserved. On the other hand the inverse function preserves both unions and intersections. |
Introduction
Parallel light shining on an object creates a shadow behind the object,
possibly falling on a wall, which defines a mapping that sends points on the
object where light strikes to its “shadow” point on a wall; i.e. the point of
continuation of the ray of light on the wall if the ray could pass through the
object. Although we can think of this map as a function sending points on the
object to points on the wall, a more useful way is to think of it as a mapping
between sets; i.e. a set of points on the surface of the object to the shadow
set on the wall.

Often in mathematics, particularly in analysis and
topology, one is interested
in finding the set of image points of a function acting on a given set, which
brings us to the following definition.
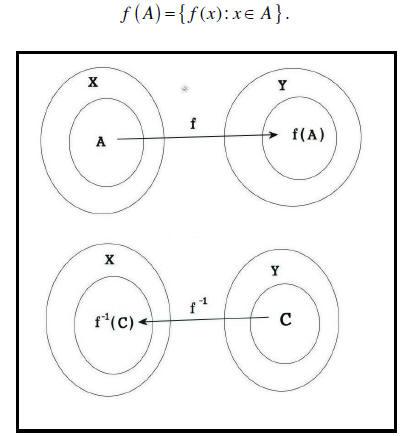
Definition: Let f : X →Y and
 . As x moves
about the set A , the set . As x moves
about the set A , the setof values f ( x) define the image of A . That is
Also if |
Example 1 Let X = {1, 2,3,4} and Y = {a,b,c} and define a
function f on
A = {1, 2,3}by f (1) = a, f (2) = a, f (3) = c . Then f ( A) = {a,c} . Also for
example 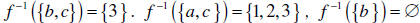 . See Figure 1.
. See Figure 1.
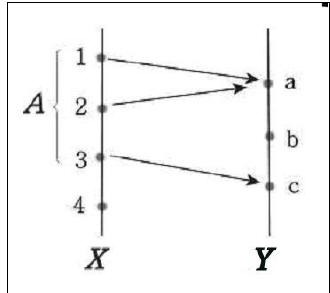
Figure 1
Example 2 Let f : X →Y be given by 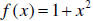 . See Figure 2.
. See Figure 2.
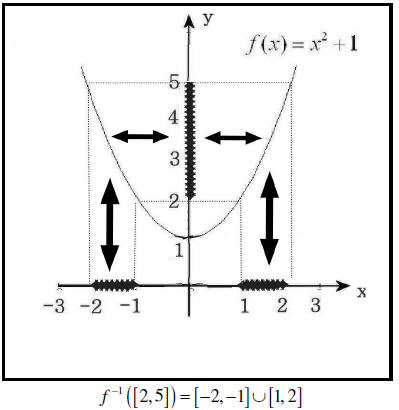
Figure 2
Then we have
a) f ({−1,1}) = {2} since both f (−1) = f (1) = 2 .
b) f ([−2,2]) = [1,5]
c) f ([−2,3]) = [1,10]
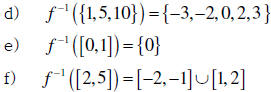
| Margin Note: It is often important to know if
certain properties of sets are preserved under certain types of mappings. For instance if X is a connected set and f a continuous function, then f ( X ) is also connected. |
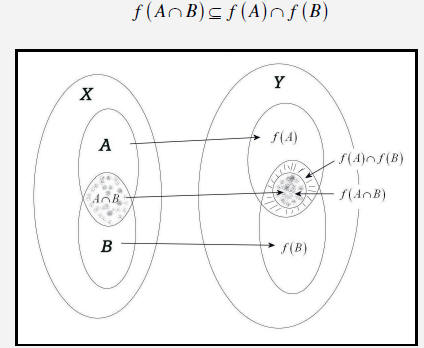
Images of Intersections and Unions
The following theorem gives an important relation of the image of the
intersection of two sets.
| Theorem 1 If f : X →Y and 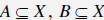 , then the images of intersections satisfy , then the images of intersections satisfy
|
Proof: Let 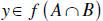 . Hence, there exists an
. Hence, there exists an
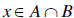 such that
such that
f ( x) = y . Hence x∈ A and x∈B . But
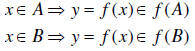
Hence 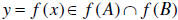 .
.
Let us now try to show the converse; that is
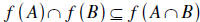 .
.
Letting  we have y∈ f ( A) and y∈ f (B) . Hence
we have y∈ f ( A) and y∈ f (B) . Hence
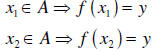
from which we conclude 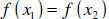 which is only
true if the function f is
which is only
true if the function f is
one-to-one. Hence, we suspect the conclusion is false in general, and thus
we look for a counterexample. That is is a non 1−1 function f X →Y and
subsets 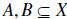 and a point
and a point
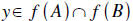 that is not in
that is not in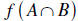 .
.
To find a counterexample let X = Y =R and A = [−1,0], B = [0,1] . Then
if f is defined by 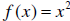 , we have
, we have
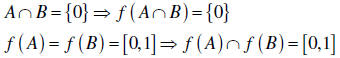
Hence 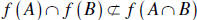 . See Figure 3.
. See Figure 3.
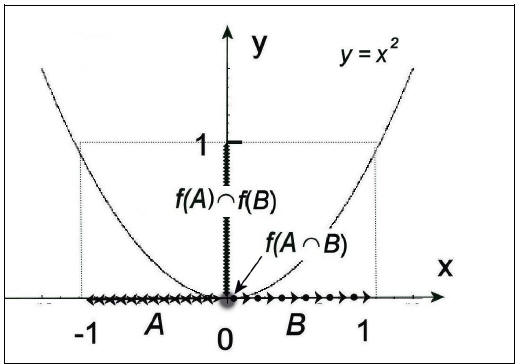
Counterexample to show 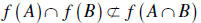
Figure 3
In general, intersections of sets are not preserved under the image of a
function. However, the following theorem shows intersections are preserved.
Theorem 2 Let f : X →Y be a one-to-one
function. If 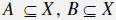 , then , thenintersection is preserved under mappings:
|
Proof: It suffices to show
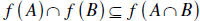 . Letting
. Letting 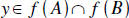 ,
,
we have y∈ f ( A) and y∈ f (B) . Hence
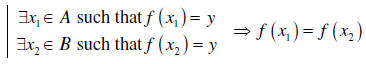
But f is assumed 1-1 so we conclude 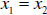 and so
and so
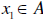 and
and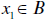 and
thus
and
thus 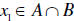
Hence 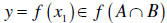 which proves theorem.
which proves theorem.



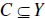 we define the
inverse image of C as
the set
we define the
inverse image of C as
the set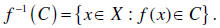
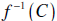 is a well defined set regardless of whether the
function f
is a well defined set regardless of whether the
function f