Quadratic Equations
Here are some possibilities
| • Both graphs start at 42 feet above the ground, so both times, Mario dropped the hammer from 42 feet. •That means that c = 42 •The blue graph starts upward. Mario was ascending in that mishap. •That means the middle coefficient is positive •The red graph starts decreasing immediately. The elevator was standing still or descending. •If it was descending, the middle coefficient is negative. •The first coefficient is -16. |
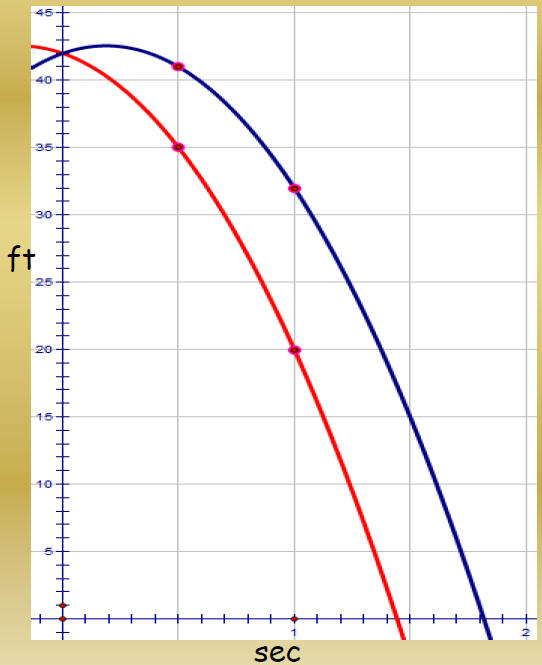 |
What we now know:
| So far, we have h(t) = -16t2 + v0t + 42. How can we find the value of the initial velocity for each graph? Let’s start with the blue graph. |
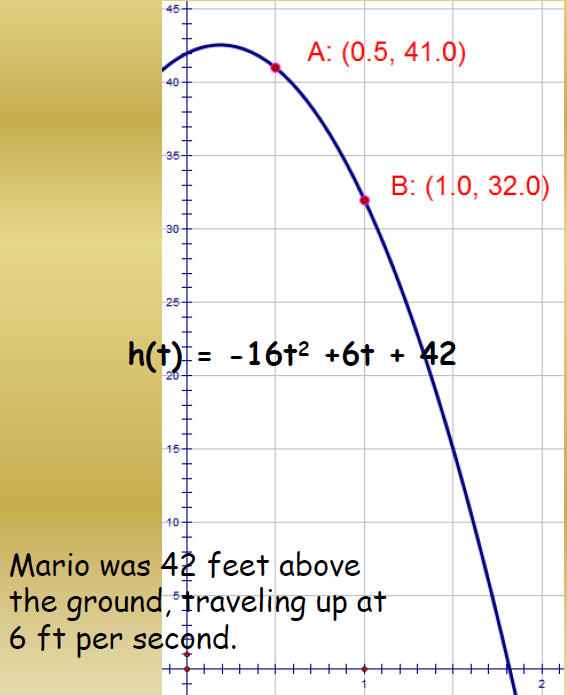 |
| Plug the values of the coordinates of one of the points into the equation: |
|
| 41 = -16(0.5)2 + v0 (0.5) + 42 41 = -4 + 42 + 0.5v0 3 = 0.5v0 v0 = 6 |
Now, you determine the equation of
the red graph
| You can use either set of coordinates h(t) = -16t2 -6t + 42 |
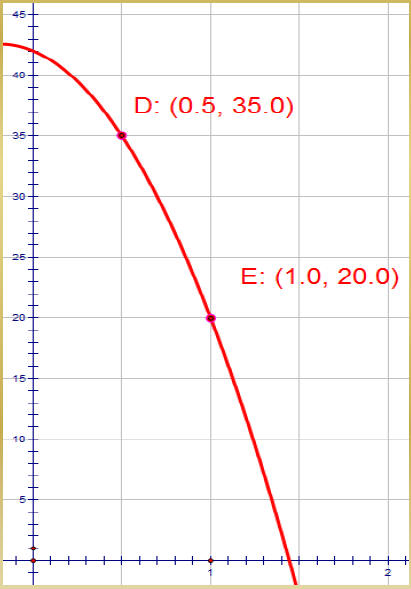 |
Let’s recap what we found
| h(t) = -16t2 +6t + 42
Blue graph shows that Mario was |
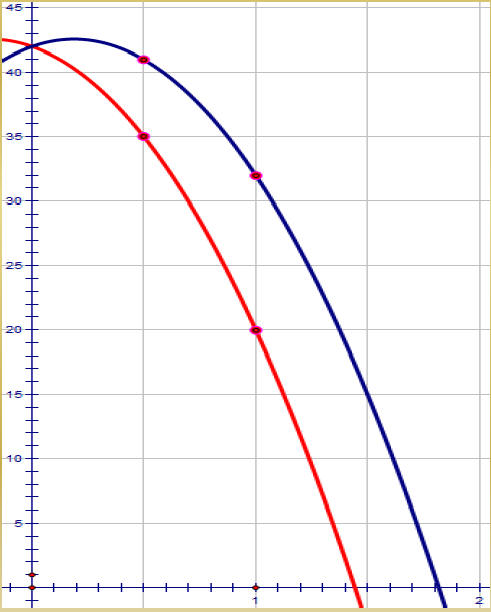 |
| h(t) = -16t2 -6t + 42
Red graph shows that Mario was |
What if a spider was riding on the
hammer?
| When Mario dropped the hammer while he was descending a spider went along for the ride. How long did the spider experience microgravity before the hammer hit the ground? |
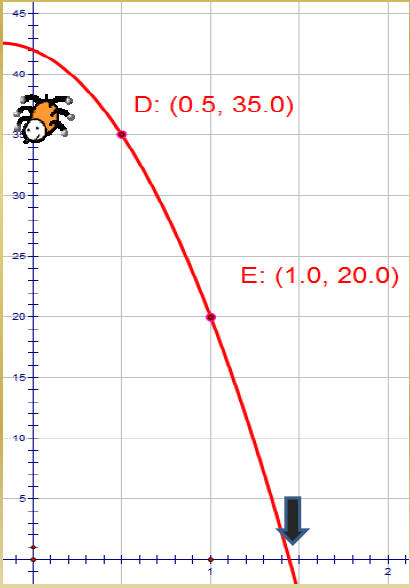 |
| Ask yourself – the hammer was how high above the ground when it hit the ground? Plug that value into the equation for h(t) and use the quadratic formula to solve for t. |
Calculate!**
How high was the hammer
above the ground when it hit
the ground?
0 feet
Plug that into the equation
For h(t).
0 = -16t2 -6t + 42
Use the quadratic
formula to solve.
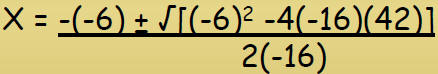
X = -1.82
x = 1.44
Since this is a real world problem
We use the positive value.
The spider was “space-spider” for 1.44 seconds
** No spiders were injured in this problem
What have you learned?
Take a moment to talk with your fellow classmates about
today’s lesson:
1. How does microgravity explain why
the astronauts appear to be “floating”
inside the space shuttle?
2. What do each of the coefficients in
the quadratic equation and the vertical
motion model represent?
3. Where on the parabolic arc do the
passengers on the parabolic flight feel
weightless?
4. If you know the equation of a vertical
motion problem, how can you tell how high an
object will be at .6 seconds?
Wrap it up!
We hope that you have
learned something from
Math Day 2009!
Oh, and of course. . .
We also hope that you enjoyed
the journey on the Vomit
Comet.
The residents of Math Land
hope that they both
entertained you and helped you
learn about microgravity.
Your teacher has an extension
problem for you to work on.
Let us know how you solve it!


