Solutions to Math Complex Problems
1. (D)
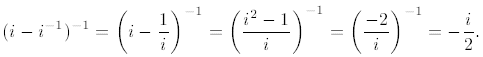
2. (B) Two given points, 1 + 2i and -1 - 2i, are symmetric
with respect to the origin,
and the distances from the origin to all three points are equal. Therefore the
origin is the
center of the square, and the fourth vertex must be symmetric to -2 + i around
it. Thus
the fourth vertex is 2 - i.
3. (B) We compute 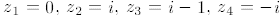 ,and
,and
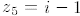 .Since
.Since 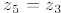 ,
it
,
it
follows that 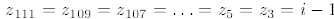 , which is
, which is
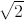 units from the origin.
units from the origin.
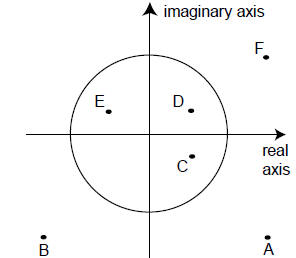
4. (C) Write F as a + bi, where we see from the diagram that a, b > 0 and a2
+ b2 > 1.
Since
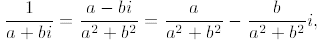
we see that the reciprocal of F is in quadrant IV, since
the real part on the right is positive
and the coefficient on the imaginary part is negative. Also, the magnitude of
the reciprocal
is
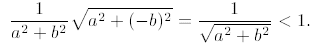
Thus the only possibility is point C.
5. (D) The set S consists of all complex numbers of the form
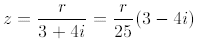
for some real number r. Since S consists of all real
multiples of 3 - 4i, each point in S is
on the line through the origin and 3 - 4i, and conversely.
6. (B) Use the quadratic formula to obtain
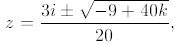
which has discriminant D = -9 + 40k. If k = 1, then D =
31, so (A) is false. If k is
a negative real number, then D is a negative real number, so (B) is true. If k =
i, then
D = -9+40i = 16+40i-25 = (4+5i)2, and the roots are 1/5+(2/5)i and
-1/5-(1/10)i,
so (C) and (D) are false. If k = 0 (which is a complex number), then the roots
are 0 and
(3/10)i, so (E) is false.
7. (D) Recall, from DeMoivre's Theorem, that the six sixth roots of -64 are
equispaced
around the circle of radius 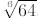 . Since ±2i are
roots, exactly two of the roots are in the
. Since ±2i are
roots, exactly two of the roots are in the
right half-plane and they must be conjugates. The product of any pair of
conjugates is the
square of their distance from the origin, so the product of these two roots is
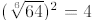 .
.
8. (E) Set z = a + bi. We seek 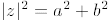 .So
.So
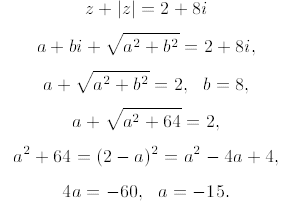
Thus, a2 + b2 = 225 + 64 = 289.
9. (B) The quadratic formula leads to the roots
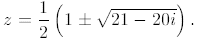
To find 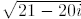 , let (a + bi)2
= 21 - 20i where a and b are real. Equating real and
, let (a + bi)2
= 21 - 20i where a and b are real. Equating real and
imaginary parts leads to a2-b2 = 21 and 2ab = -20. Solve
these equations simultaneously:
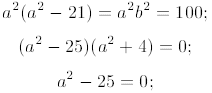
so a = ±5 and b = 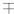 2.
Thus a + bi = 5- 2i or -5 + 2i. Therefore,
2.
Thus a + bi = 5- 2i or -5 + 2i. Therefore,
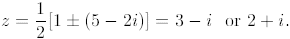
The product of the real parts of these two roots is -6.
10. (C) Note that x3 = y3 = 1, because x and y are the
complex roots of 0 = x3- 1 =
(x-1)(x2+x+1). Alternatively, plot x and y in the complex plane and
observe that they
have modulus 1 and arguments 2π /3 and 4π /3, Thus x9 + y9
= 1+1 ≠ -1.


