Polynomial Functions

PURPOSE

This lesson covers polynomial functions. The graphing, writing, and use of the functions are
stressed.

OBJECTIVES

After completing this lesson, you should be able to

• identify a polynomial function;

• evaluate a polynomial function using synthetic division and determine its zeros;

• use synthetic division to apply the remainder and factor theorems;

• graph a polynomial function and determine an equation for a polynomial graph;

• write a polynomial function for a given situation and find the maximum or minimum value of
the function;

• use technology to approximate the real roots of a polynomial equation;

• solve polynomial equations by various methods of factoring and the RATIONAL ROOT
THEOREM; and

• apply several theorems about polynomial functions.

READING ASSIGNMENT

Chapter 2, Sections 2-1 through 2-7 (pages 53–93)

COMMENTARY

Section 2-1: Zeros and Factors of Polynomial Functions, pp. 53–58

A polynomial function involves an equation that can be written in the following form:

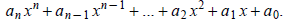
The powers of x can be any number, and they should be written in decreasing order. Examples of
polynomials follow with key terms for each.

Equation	Degree	coefficient	Constant	Leading coefficient	Terms

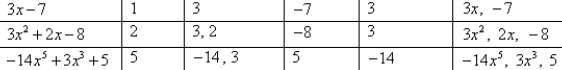The roots of a polynomial function are x-values that give the function a value of zero. The roots of
P (x) = 3 x − 7 and P (x) = 3 x² + 2 x − 8 are found below:

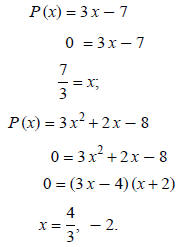
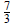is a root and a zero for P (x) = 3 x − 7.

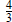and −2 are roots and zeros for P (x) = 3 x² + 2 x − 8.

Other values of the function can be found by placing desired values into the function.

Example 1: Find P (−3) given P (x) = 2 x² − 4 x + 6:

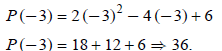
Example 2: Let's try problem 18b on page 56 of your text.

Find k (1 + i) given k(x) = x² (x² + 16)
 

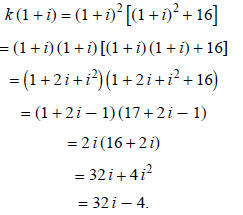
Synthetic substitution is another method that can be used to find values of functions. I will use
synthetic substitution to determine the value of f (−5) when f (x) = 2 x³ − 3 x² + 4 x + 5.

List all of the coefficients. Drop the leading coefficient down, multiply 2 by −5, and place in the
box:

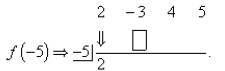
Add −3 and −10. Multiply −13 by −5 and place in the box:

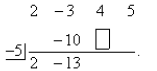
Add 4 and 65. Multiply 69 by −5 and place in the box:

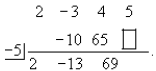
Add 5 and −345:

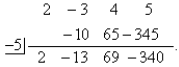
The result is −340, so f (−5) = − 340.

Let's check it out:

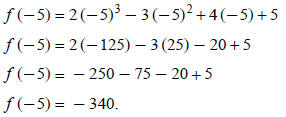
For this problem, synthetic substitution would have been the quicker method. The synthetic
substitution can be done in one step as follows

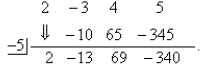
Example 3: Use synthetic substitution to find P (−2) when P (x) = x⁵ − 1.

There are several missing terms in x⁵ − 1. The complete polynomial equation is
x⁵ + 0 x⁴ + 0 x³ + 0 x² + 0 x − 1. All terms must be used in synthetic substitution:

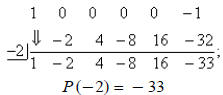
In this problem P (−2) = (−2)⁵ − 1, but −32 − 1 = − 33 is quicker. Which method would be
quicker for P (−1) = x¹⁵ − 2? Think of all the missing terms! This would be quicker using
substitution. Use the method best suited for the situation.

Example 4: Let's try problem 24 on page 57 of your text.

If 2i is a zero, then f (2i) = 0:

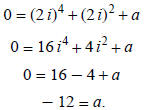
Example 5: Let's try problem 30b on page 57 of your text.

Given g (x) = 3 − 8 x, find g (x + 2) − g (x):

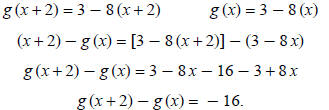
Study Exercises

Complete odd-numbered problems 1–27 in the Written Exercises section on pages 56–57 of your
text. Then check your answers in the back of the text.

Section 2-2: Synthetic Division: The Remainder and Factor Theorems, pp. 58–61

Synthetic substitution is versatile. Used not only to find the value of a function, it can also be used to
find the quotient and remainder in a polynomial division problem. When it is used in this manner, it
is referred to as synthetic division. I will work through a polynomial division problem and compare
the results to those in a corresponding synthetic division.

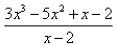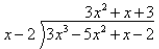			Multiply
	subtract
	subtract		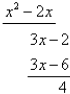Multiply
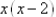			Multiply
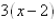	subtract
			remind

Since I divided by x − 2, I will use 2 in my synthetic division. If I had divided by x + 3, I would
have used −3 in my synthetic division:

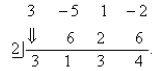
The remainder is 4 and 3 x² + 1 x + 3 is the quotient.

If the binomial x − 2 would have been a factor of 3 x³ − 5 x² + x − 2, the remainder would have
been zero. So if my only desire is to determine if x − 2 is a factor of 3 x³ − 5 x² + x − 2, I don't need
to divide it out. I could use synthetic division and just look at the remainder. Or, I could use
substitution. In this case, I would find P(2) given P(x) = 3 x³ − 5 x² + x − 2:

P(2) = 3 (2)³ − 5 (2)² + 2 − 2.

P(2) = 4 is the same as the remainder.

This demonstrates the REMAINDER THEOREM.

So, depending on the problem, I could choose synthetic division or substitution to determine if x − a
is a factor of P(x). If I wish to divide a polynomial by a polynomial of a degree higher than 1, I need
to use long division.