Introduction to Number Theory Review Sheet for Exam #2
• Linear diophantine equations and Least common multiple
– What is a linear diophantine equation? Given an equation
in two unknowns with
integer coefficients, how do you know whether it is has any integer solution?
Can it
have infinitely many positive integer solutions?
– What is a common multiple of two integers a and b? What is their least common
multiple? Is there any relationship between greatest common divisor and least
common
multiple?
– Suggested problems:
1. For linear diophantine equations, see the exercises posted for Quiz 2.
2. Compute lcm(−357, 629) and lcm(299, 377, 403).
3. Write down any two or three nonzero integers, and ask yourself what’s their
least
common multiple.
4. If a and b are relatively prime, what can lcm(a + 2b, 2a + b) be?
• Prime numbers and Special numbers
– What is a prime number? Can you name some? What is a
composite number? Can
you name some? Given an integer greater than 1, how can you tell whether it is
prime
or composite? How many primes are there?
– What does the Fundamental Theorem of Arithmetic say? Can we use it to find
greatest
common divisor and least common multiple?
– What is a twin prime? A Mersenne prime/number? A Fermat prime/number? A
perfect number? How are Mersenne primes and perfect numbers related?
– What is the -function? The
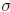 -function? Given an integer n, can you find
-function? Given an integer n, can you find
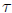 (n)
and
(n)
and
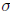 (n)?
(n)?
– Suggested problems:
1. Compute lcm(−357, 629) and lcm(299, 377, 403).
2. Compute
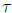 (4725)
and
(4725)
and
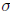 (4725).
(4725).
3. Compute
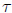 (3718)
and
(3718)
and
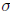 (3718).
(3718).
4. Write an − 1 (respectively an + 1) as a product of two factors in terms of
a.
5. Let q = 2n-1 · p, where p = 2n − 1 is a Mersenne prime. List all the
divisors of q
and show directly that q is a perfect number.
• Equivalence relations
– What are the three properties characterizing an equivalence relation? Given a
relation,
can you determine whether it is an equivalence relation? Remember that if it
is, you have to “proof” all three properties. But if it isn’t, you only need to
give one
counterexample.
What is an equivalence class? What is a representative of an equivalence class?
– Suggested problems:
1. Which of the following are equivalence relations? Justify your answers.
(i) The relation of parallelism for lines.
(ii) The relation of “less than or equals” for real numbers.
(iii) The inclusion relation for sets.
(iv) The equality relation for sets.
2. Criticize the following argument that the reflexive property for equivalence
relations
is a consequence of the symmetric and transitive properties: According
to the symmetric property, if aRb, then bRa. Then according to the transitive
property with the c in the definition replaced by a, aRa and the relation R is
reflexive if it is symmetric and transitive.
• Basics of congruences
– What does it mean for two integers to be congruent modulo m? Given an integer
a,
can you find its least residue modulo m? Can you list some residues of a modulo
m?
– Since congruence of integers is an equivalence relation, it partitions the set
of all integers
into disjoint subsets. What are these subsets called? How many such subsets are
there?
Can you describe them (i.e. listing all the elements in each subset)?
– Do you know what is the least residue system modulo m and a complete residue
system
modulo m? Given a set of integers, can you determine whether it is a complete
residue
system modulo m? Can you write down some complete residue systems modulo m?
– Are you familiar with the basic properties of congruence of integers? Do you
know how
congruences behave when we do addition and multiplication? Can you make use of
these properties of congruences to help make calculation of least residues
simpler?
– Suggested problems:
1. Find the least residue of 22 · 51 + 6985 modulo 7.
2. Find the least residue of 32 and 320 modulo 5.
3. Prove that the Mersenne number 237−1 is divisible by 223, that is, 237≡1 (mod
223).
4. Show that the numbers −13, −9, −4, −1, 9, 18, 21 form a complete residue
system modulo 7.
5. Find a complete residue system modulo 5 composed entirely of negative odd
integers.
6. Prove that a perfect square must have one of 0, 1, 4, 5, 6 or 9 for its units
digit.
(Hint: An integer is congruent modulo 10 to its units digit.)
• Divisibility tests
– What is the decimal representation of an integer?
– How can you decide whether a given integer is divisible by 2, 3, 5, 9 and 11?
From
there, can you tell if an integer is divisible by say 4, 6, 99, etc?


