Equations Containing Rational Expressions

Chapter 7: Section 1 Radical Expressions

Every positive real number has 2 square roots–one that is positive
(which is called the principal square root)of the number and one
that is negative.

EX1. What are the square roots of 25? What is the principal square
root of 25?

EX2. What are the square roots of 10? What is the principal square
root of 10?

The square roots of negative real numbers are complex (not real)
numbers.

EX3. Explain why 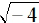is not a real number.

If a > 0, 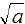then denotes the principal square root of a.

EX4.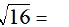
EX5.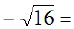
EX6.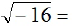

(Be careful when taking the square root of variables unless you are
told that the variables represent positive real numbers.)

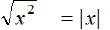for all real numbers x.
If x > 0, then 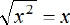but if x < 0, the 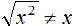. To ensure
that 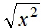is never negative, we use |x|.

EX7.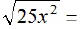

EX8.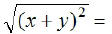

The cube root of a number a, denoted by 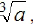is a number b such
that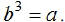

EX9. Explain why 2 is a cube root of 8 but 4 is not.

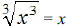for all real numbers. [Why don’t we use absolute value
bars around x here like we did for square roots?]

EX10.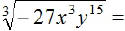

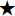In general, the nth root of a, denoted by 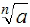, is a number b such
that 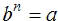. [The nth root of a may not always be a real number.]

EX11.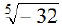

EX12.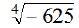

EX13.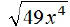

EX14.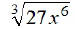

The graph of the square root function 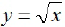is shown below.

What is the domain of this function?

What is the range of this function?

EX15. Graph 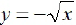and find its domain and range.

EX16. Graph 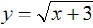and find its domain and range.

EX17. Graph 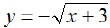and find its domain and range.

EX18. Graph 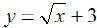and find its domain and range.

EX19. Graph 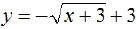and find its domain and range.

EX20. The height of a cylinder is given by the formula: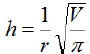

where V represents the volume of the cylinder and r is its radius.

Find the height of a cylinder whose radius is 3 cm and whose
volume is 16π cubic cm.

Find the volume of a cylinder whose height is 5 inches and whose
radius is 2 inches.

Chapter 7: Section 2 Application of Radicals

Pythagoras

1) Born about 575 B.C. on the Greek island of
Samos.

2) The first man to call himself a philosopher–a lover of
wisdom.

3) Founded the Pythagoreans in Croton in southern Italy.

4) The Pythagoreans believed in metempsychosis–a belief
that the soul in reincarnated into the bodies of humans,
animals, and vegetables.

5) Although the Pythagoreans were vegetarians, they didn’t
believe in eating beans. One possible explanation for this
is they believed that every time you farted part of your soul
was lost.

6) Died about 435 B.C.

The Pythagorean Theorem states: _______________________________
__________________________________________________________
__________________________________________________________
__________________________________________________________
__________________________________________________________
__________________________________________________________

EX1. Find the from one corner of a room to the diagonally opposite
corner if the room is rectangular in shape and is 15 ft by 22 ft.

EX2. A ladder that is 17 feet long is leaning against a house. If the
ladder is placed 7 feet from the base of the house, how far up on
the side of the house does the ladder reach?

EX3. How are from the base of a house should you put a 22 ft ladder
if you want to reach a window that is 16 feet above the ground?

EX4. A baseball field is in the shape of a diamond (square) that is 90
ft on each side. How far is it from home plate to second base?

One of the many proofs of the Pythagorean Theorem was discovered by
James A. Garfield, the twentieth president of the United States.

1) Born on November 19, 1831. Last president to be born in
a log cabin.

2) In 1857 was named president of Hiram College in Ohio.

3) In 1858, he married Lucretia Randolph. They had 7
children.

4) Served as a major general in the Civil War.

5) In 1876, he discovered an original proof of the Pythagorean
theorem.

6) Was elected the twentieth president of the United States
of American in 1880.

7) Shot twice on July 2, 1881. Died on September 19, 1881.

The converse of the Pythagorean Theorem states: __________________
__________________________________________________________
__________________________________________________________
__________________________________________________________
__________________________________________________________

EX5. If the lengths of the sides of a triangle are 5 cm, 12 cm, and 13
cm is the triangle a right triangle? Justify your answer.

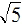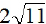EX6. If the lengths of the sides of a triangle are ft, ft, and
7 ft is the triangle a right triangle? Justify your answer.

EX7. Suppose that x and x+3 are two sides in a right triangle whose
hypotenuse is 15 m. Find the lengths of these two sides.

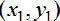Let and 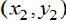be the coordinates of two points. The
distance between these points is given by the formula:

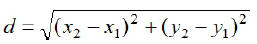
EX8. Find the distance between the following pairs of points.

(3, 4) and (2, 11)

(-1, -6) and (-4, -9)

A scalene triangle is ____________________________________
_____________________________________________________.

An isosceles triangle is __________________________________
_____________________________________________________.

An equilateral triangle is ________________________________
_____________________________________________________.

EX9. Find the length of each side of the triangle whose vertices are
(-2, 1), (-1,5), and (4,2). Classify this triangle as either scalene,
isosceles, or equilateral.