Properties of Geometric Shapes

In this section we study the properties of geometric shapes that belong to
the same plane such as lines and angles.

Lines
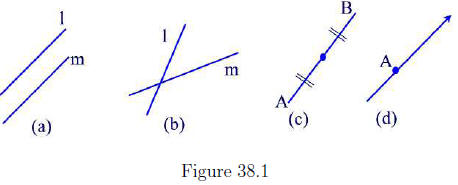
Two lines in a plane that do not have a point in common are called parallel.
See Figure 38.1 (a). If the two lines are l and m then we write l| |m. When
two or more lines have exactly one point in common then we say that they
are concurrent. See Figure 38.1(b).

The midpoint of a line segment is a point that is equidistant from A and
B, that is a point that has the same distance from A and B. See Figure
38.1(c). A ray is a subset of a line that contains the endpoint and all points
on the line on one side of the point. See Figure 38.1(d).

Next, we list some of the important properties of lines.

Properties
(1) Through any distinct two points there is exactly one line going through
them.
(2) If two points are in a plane then the line containing them lies in that
plane.
(3) There is exactly one plane containing any three noncollinear distinct
points.
(4) A line and a point not on the line determine a plane.
(5) Two parallel lines determine a plane.
(6) Two concurrent lines determine a plane.

Angles: Measurements and Types
We have seen that an angle is the opening between two line segments with
one common endpoint. An angle can be also defined as the opening between
two rays with the same endpoint called the vertex. We call the rays
the sides of the angle. If A is the vertex, B is a point on one side and C is
a point on the other side then we write∠BAC. See Figure 38.2. Note that
the middle letter in the notation of an angle is always the vertex. Sometimes
only the vertex A is given. In this case we use the notation∠A. Also, angles
can be labeled using numbers. In this case we use the notation∠1 to denote
the angle labeled 1.

An angle is measured according to the amount of ”opening” between its
sides. A unit of angle measure is the degree. A complete rotation about a
point has a measure of 360 degrees, written 360° . Thus, one degree is 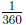of
a complete rotation. We will write m(∠BAC) for the measure of the angle
at vertex A.

Angles are measured using a protractor. To measure an angle ∠BAC, place
the center of the protractor at the vertex A while lining up the side AB with
the base of the protractor. The other side of the angle will pass through
a number on the protractor representing m(∠BAC) in degrees. See Figure
38.2.

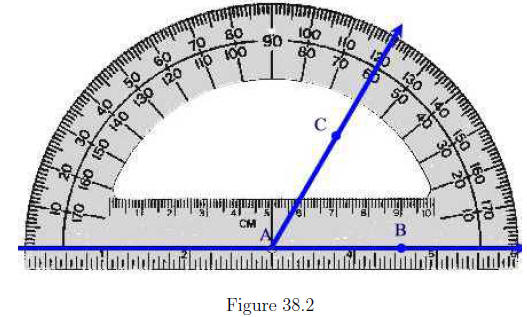
Next, we categorize angles according to their measures. If m(∠BAC) =
90° then we will say that the angle is a right angle. See Figure 38.3(a).
Two lines that intersect at a right angle are called perpendicular. If
m(∠BAC) = 180° we say that the angle is straight. See Figure 38.3(b). If
0° < m(∠BAC) < 90° then the angle is called acute. See Figure 38.3(c). If
90° < m(∠BAC) < 180° then the angle is called obtuse. See Figure 38.3(d).
If m(∠BAC) > 180° then the angle is called reflex. See Figure 38.3(e).

Now, recall that a triangle has three interior angles. If one of the angles is a
right angle then we call the triangle a right triangle. If one of the angle is
obtuse then we call the triangle an obtuse triangle. If all three angles are
acute angles then the triangle is called an acute triangle.

Pairs of Angles and the Vertical Angles Theorem
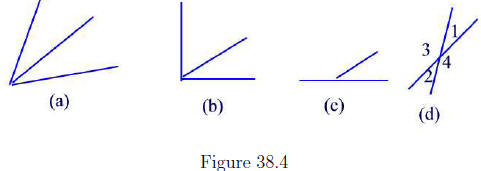
Two angles that have a common side and nonoverlapping interiors are called
adjacent angles. See Figure 38.4(a). If the sum of two adjacent angles is
90° then the two angles are called complementary. See Figure 38.4(b).
Two adjacent angles whose sum is 180° are called supplementary angles.
See Figure 38.4(c). A pair of nonadjacent angles formed by two intersecting
lines are called vertical angles. For example, m(∠1) and m(∠2) are vertical
angles as well as m(∠3) and m(∠4). See Figure 38.4(d)

Vertical angles are congruent as shown in the following theorem.

Theorem 38.1 (Vertical Angles Theorem)
Vertical angles have the same measure.

Proof.
The angles ∠1 and ∠3 are supplementary so that m(∠1) + m(∠3) = 180° .
Similarly, the angles ∠2 and ∠3 are supplementary so that m(∠2)+m(∠3) =
180 . Thus, m(∠1)+m(∠3) = m(∠2)+m(∠3). Subtracting m(∠3) from both
sides of the equation gives m(∠1) = m(∠2). A similar argument shows that
m(∠3) = m(∠4)

Angles Associated with Parallel Lines
If two lines k and l are parallel then a line m as shown in Figure 38.5 is
called a transversal line. In this case, there are 8 angles determined by
these three lines numbered 1 through 8.

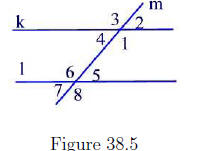
Angles∠1 and ∠6 as well as angles ∠4 and ∠5 are called alternate interior
angles. The following theorem shows that any pair of alternate interior
angles are congruent.

Theorem 38.2
Any pair of alternate interior angles have the same measure.

Proof.
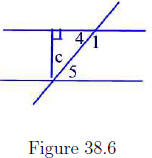
We will show that m(∠4) = m(∠5). The other equality is similar. According
to Figure 38.6 we have the following equalities: m(∠c) + m(∠5) = 90° and
m(∠4)+m(∠c) = 90° . Thus, m(∠c)+m(∠5) = m(∠4)+m(∠c). Subtracting
m(∠c) from both sides we obtain m(∠4) = m(∠5)

Now, going back to Figure 38.5, the angles ∠1 and ∠8; ∠2 and ∠5; ∠3 and ∠6;
∠4 and ∠7 are called corresponding angles. Every pair of corresponding
angles are congruent as shown in the next theorem.

Theorem 38.3
Corresponding angles have the same measure.

Proof.
We will just show that m(∠2) = m(∠5). By the vertical angles theorem we
have m(∠2) = m(∠4). By the alternate interior angles theorem we have
m(∠4) = m(∠5). From these two equalities we conclude that m(∠2) =
m(∠5)

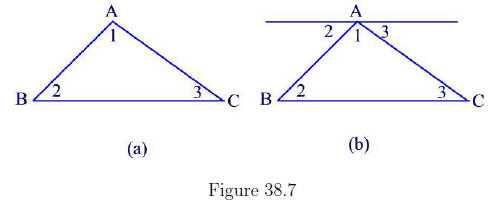
Sum of the Measures of the Interior Angles of a Triangle
As an application to the results of the previous paragraph, we show that the
sum of the measures of the interior angles of a triangle is 180° . To see this,
let’s consider a triangle with vertices A, B, and C and interior angles ∠1,∠2,
and ∠3 as shown in Figure 38.7(a). At A draw a line parallel to the line
segment . Then using the corresponding angles theorem we can draw
Figure 38.7(b) which shows that

m(∠1) + m(∠2) + m(∠3) = 180°
as required.

Practice Problems

Problem 38.1
Using Figure 38.5 show that m(∠1) + m(∠5) = 180° .

Problem 38.2
(a) How many angles are shown in the following figure?

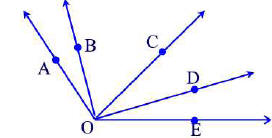
(b) How many are obtuse?
(c) How many are acute?

Problem 38.3
Find the missing angle in the following triangle.

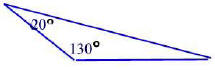
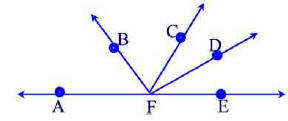
Problem 38.4
In the figure below, m(∠BFC) = 55° ,m(∠AFD) = 15°0 , m(∠BFE) =
120° . Determine the measures of m(∠AFB) and m(∠CFD).

Problem 38.5
In the following figure 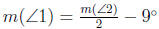. Determine m(∠1) and m(∠2).

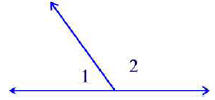
Problem 38.6
Angles 3 and 8; 2 and 7 in Figure 38.5 are called alternate exterior angles.
Show that m(∠3) = m(∠8).

Problem 38.7
Following are the measures of ∠A,∠B,∠C. Can a triangle ΔABC be made
that has the given angles? Explain.

(a) m(∠A) = 36° ,m(∠B) = 78° ,m(∠C) = 66° .
(b) m(∠A) = 124° ,m(∠B) = 56° ,m(∠C) = 20° .
(c) m(∠A) = 90° ,m(∠B) = 74° ,m(∠C) = 18° .

Problem 38.8
In the following figure 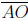is perpendicular to 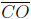. If m(∠AOD) = 165° and
m(∠BOD) = 82° , determine the measures of ∠AOB and ∠BOC.

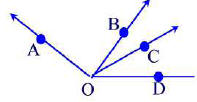
Problem 38.9
In the figure below, find the measures of ∠1,∠2,∠3, and ∠4.

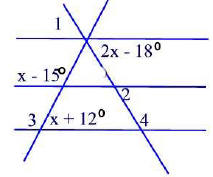
Problem 38.10
(a) How is a line segment different from a line?
(b) What is the vertex of the angle ∠PAT?
(c) How is 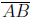different from AB?

Problem 38.11
A fourth grader thinks that m(∠A) is greater than m(∠B).

(a) Why might the child think this?
(b) How could you put the angles together to show that m(∠A) < m(∠B)?

Problem 38.12
In the figure below

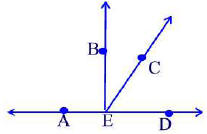
(a) name two supplementary angles
(b) name two complementary angles.

Problem 38.13
An angle measures 20° . What is the measure of
(a) its supplement? (b) its complement?

Problem 38.14
True or false? If false give an example.

(a) All right angles are congruent.
(b) Two complementary angles are congruent.
(c) Two supplementary angles are congruent.

Problem 38.15
Find the measures of the angles in the following figure.

Problem 38.16
How many degrees does the minute hand of a clock turn through

(a) in sixty minutes?
(b) in five minutes?
(c) in one minute?

Problem 38.17
How many degrees does the hour hand of a clock turn through

(a) in sixty minutes?
(b) in five minutes?

Problem 38.18
Find the angle formed by the minute and hour hands of a clock at these
times.
(a) 3:00 (b) 6:00 (c) 4:30 (d) 10:20

Problem 38.19
Determine the measures of the interior angles.

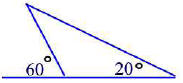
Problem 38.20
(a) Can a triangle have two obtuse angles? Why?
(b) Can a triangle have two right angles? Why?
(c) Can a triangle have two acute angles?

Problem 38.21
A hiker started heading due north, then turned to the right 38° , then turned
to the left 57° , and next turned right 9°. To resume heading north, what turn
must be made?