Fractions

Directions: Please read very carefully. Complete all of the problems.
Show all of your work. You may NOT use a calculator

A fraction represents a part out of a whole. Normally the numerator (top half) of the
fraction is smaller than the denominator (bottom half). This is called a proper fraction,
a number less than 1.

Practice: Represent the shaded portion of each shape with a fraction.

Sometimes the numerator is equal to or larger than the denominator. This is called an
improper fraction, a number equal to or greater than 1.

Each small portion above represents one-fourth of a rectangle. There are 13 fourths,
which can be written as the improper fraction13/4 or as the mixed number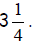

Convert the following improper fractions to a mixed number.

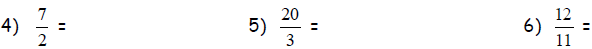
Convert the following mixed numbers to improper fractions.


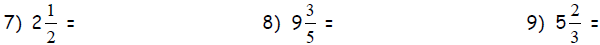
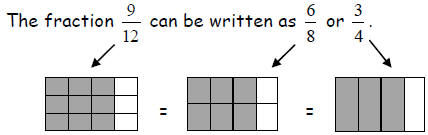
All three fractions represent the same piece of the rectangle. There is an infinite
(endless amount) of fractions equivalent to any given fraction.

For example, the fraction

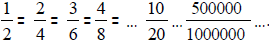
Practice: Determine the value of the question mark that would create an equivalent
fraction.

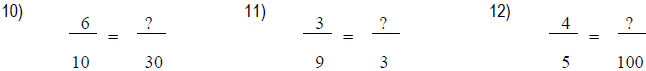
Fractions can also be written in simplest form (reduced). For example, 50/100 can be
reduced to ½.

Practice: Reduce the following fractions.

When adding or subtracting fractions you need to find change each fraction by creating
equivalent fractions with the same denominator. Next, you add or subtract the
numerators, keeping the common denominator. Always make sure that your solution is
written in simplest form and in proper form. For example,

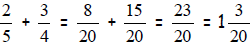
Practice: Find the sum (answer to an addition problem) or the difference (answer to a
subtraction problem.

When multiplying fractions you do not need a common denominator. To find the new
numerator, you simply multiply the numerators. To find the new denominator, you simply
multiply the denominators. Finally, always reduce your answer. For example,
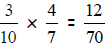which reduces to

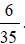
Dividing fractions is trickier. Always remember to KEEP, CHANGE, and REARRANGE.
You KEEP the first fraction the way it is. You CHANGE the division sign to a
multiplication sign. REARRANGE the second fraction by taking the reciprocal of the
fraction (flipping it). Finally, multiply like you did above. Make sure to reduce.
For example, 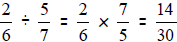which reduces to

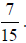
Directions: Please read very carefully. Complete all of the problems.
Show all of your work. You may use a calculator.

There are different ways to write the same number. For example, the fraction ½ can
be written as the decimal, 0.5, or the percent, 50%.

A fraction is also a division problem. To convert a fraction to a decimal, you must divide
the numerator by the denominator.

For example, ¼ is equal to 1 ÷ 4 which is equal to 0.25.

To convert a decimal to a percent, you simply multiply the decimal by 100 (moving the
decimal place to the right two places).

For example, 0.25 is equal to 25%.

Practice: Convert the following fractions to decimals, rounding the decimal to the
nearest hundredth place. Then, convert the decimal to a percent.
29) 3/8  = _________ = _________
31) 11/7 = _________ = _________
30) 5/12 = _________ = _________
32) 8/15 = _________ = _________

Fraction/Percent Word Problems:
33) Mr. Wagner’s class contains 18 girls out of 29 students. What percent of Mr.
Wagner’s class are girls? Show your work.

34) An orange juice mixture contains 20% concentrate and 80% water. If the
mixture contains a total of 50 ounces of liquid, how many ounces of
concentrate are in the mix? How many ounces of water are in the mix? Show
your work.

Use the correct formula from above to help you answer the following questions.

Find the area, perimeter, or circumference of the following shapes.
35)


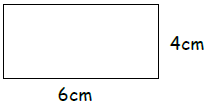
Area - _____________
Perimeter - _________

36)

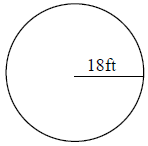
Area - _____________
Perimeter - _________

37) A square with a length of 12cm.
Area - _____________
Perimeter - _________

38)

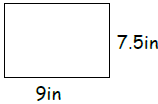
Area - _____________
Perimeter - _________

39)

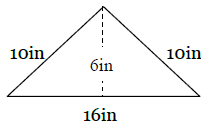
Area - _____________
Perimeter - _________

40) A circle with a diameter of 20ft.
Area - _____________
Perimeter - _________