Finding Solutions of Polynomial Equations
Factoring Method - Some, but not all polynomial equations can be
solved by factoring.
Later on in the course we will learn another method.
•Bring all terms of the polynomial equation to one side so that the other side
is equal
to 0. Combine like terms, if necessary.
•Factor relative to the integers.
•Apply the Zero Product Principle.
Problem 1:
Solve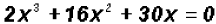 
. Find all
solutions, real and imaginary!
First, we will factor out the greatest common factor.
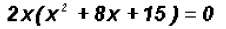
Then, we will factor the trinomial as follows:
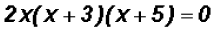
Using the Zero Product Principle, we find
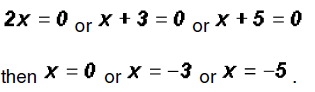
We find that the polynomial equation has 3 real solutions!
Problem 2:
Solve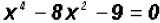 
. Find all
solutions, real and imaginary!
Sometimes, you can encounter polynomial equations that are
quadratic in form. That is,
one exponent is exactly twice as large as the other exponent!
We can rewrite the first variable as follows:
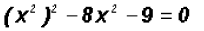
Then we factor.
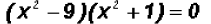
Using the Zero Product Principle and using the Square Root Property, we get
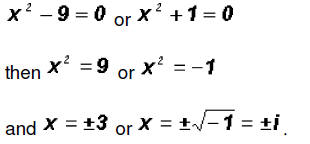
We find that the polynomial equation has 2 real solutions and 2 imaginary solutions!
Problem 3:
Solve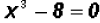 
. Find all
solutions, real and imaginary!
Notice that we are dealing with a Difference of Cubes
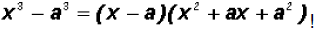
In our case, a = 2, therefore, we can factor as follows:
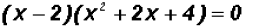
Using the Zero Product Principle we will solve as follows.
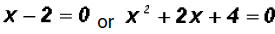
The solution for the first factor is
.
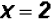Using the Quadratic Formula for the second factor we get
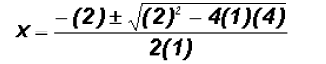
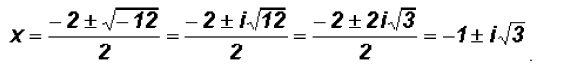
We find that the polynomial equation has 1 real solution and 2 imaginary solutions!
Problem 4:
Solve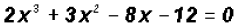 
. Find all
solutions, real and imaginary!
In this case, factoring is not readily apparent. Here, we
will try to group two terms and
then we will try to factor the common factor out of the first two terms and out
of the last two!
This is called factoring by grouping!
Let's group the first two terms and the last two terms:
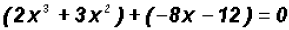.Notice that you group
by enclosing the terms in
parenthesis. Observe how the last two terms were grouped!
We notice that the first two terms have a
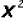in common and the last two terms have - 4.
We will factor out the common factor of the first two terms and of the last two!
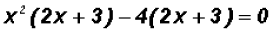
Notice that (2x + 3) is a factor of the first term and the second term. Factor it out!
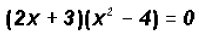
We notice that the second term is a Difference of Squares
so that we can state the
following:
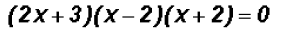
Using the Zero Product Principle we will solve as follows.
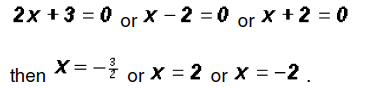
We find that the polynomial equation has 3 real solutions!
Problem 5:
Solve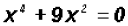 
. Find all
solutions, real and imaginary!
First, we will factor out the greatest common factor.
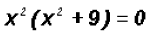
Using the Zero Product Principle, we find
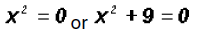
Solving the first factor, we find that
.
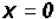Solving the second factor using the Square Root Property, we find that
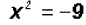, which results in
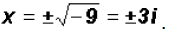
We find that the polynomial equation has 1 real solution and 2 imaginary solutions!
Problem 6:
Solve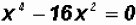 
. Find all
solutions, real and imaginary!
First, we will factor out the greatest common factor.
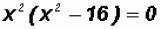
We notice that the second term is a Difference of Squares
so that we can state the
following:
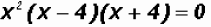
Using the Zero Product Principle, we find
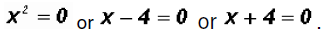
Solving the first factor, we get
.
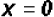Solving the second and third factor, we get
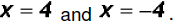
We find that the polynomial equation has 3 real solutions!
Problem 7:
Solve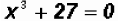 
. Find all
solutions, real and imaginary!
Since the degree of the polynomial is three, we must find three Zeros, not
necessarily
distinct.
Notice that we are dealing with a Sum of Cubes
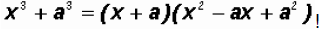
In our case, a = 3, therefore, we can factor as follows:
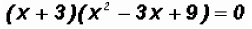
Using the Zero Product Principle we set each factor equal to 0 and solve.
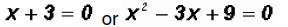
The solution for the first factor is
.
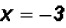Using the Quadratic Formula for the second factor we get
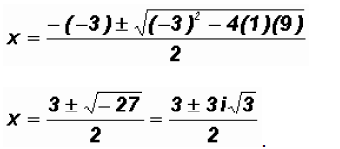
We find that the polynomial equation has 1 real solution and 2 imaginary solutions!
Problem 8:
Solve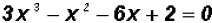 
. Find all
solutions, real and imaginary!
In this case, factoring is not readily apparent. Here, we
will try to group two terms and
then we will try to factor the common factor out of the first two terms and out
of the last two!
This is called factoring by grouping!
Let's group the first two terms and the last two terms:
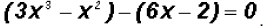Notice that you group
by enclosing the terms in
parenthesis. Observe how the last two terms were grouped!
We notice that the first two terms have a
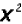in common and the last two terms have -2.
We will factor out the common factor of the first two terms and of the last two!
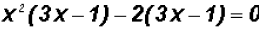
Notice that (3x - 1) is a factor of the first term and the second term. Factor it out!
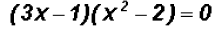
Using the Zero Product Principle we will solve as follows:
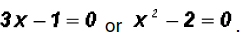
The solution for the first factor is
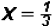
and using the Square Root Property for the second factor we get
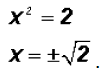
We find that the polynomial equation has 3 real solutions!
Problem 9:
Solve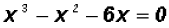 
. Find all
solutions, real and imaginary!
First, we will factor out the greatest common factor.
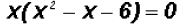
Then, we will factor the trinomial as follows:
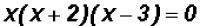
Using the Zero Product Principle, we find
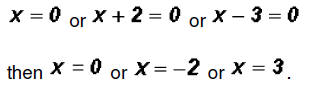
We find that the polynomial equation has 3 real solutions!