Math 327A Exercise 2
1. The decreasing sequence
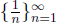converges to 0. What can you say about the sequence
{1/3, 1/2, 1, 1/6, 1/5, 1/4, 1/9, 1/8, 1/7, ...}?
Solution: The sequence is not decreasing, but its limit is still 0. If we
call the sequence
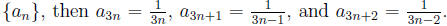Those terms go to zero as n goes to
infinity.
One can also appeal to the fact that the sequence {1/3, 1/2, 1, 1/6, 1/5,
1/4, 1/9, 1/8, 1/7, ...}
is a rearrangement of the decreasing sequence
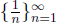which converges to 0. By the fourth
exercise of the first assignment, the rearranged sequence converges to the same
limit as the
original series.
2(a). Suppose that the sequence
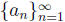is a list of t he rational numbers between 0 and 1.
(The sequence is a rearrangement of the sequence in part b.)
Show that every real number between 0 and 1 is the limit of some convergent
subsequence
of
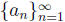
Solution: Let r be a real number in the range 0 < r < 1. We will find
a increasing
subsequence of
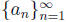that converges to r. Let s1 be a rational number between r/2 and
r (There is an infinity number of such rational numbers by the first exercise
set). Because
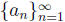is a list of the rational numbers,
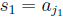for some index j1. Excluding the
numbers
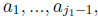, there are an infinite number of rational
numbers between
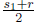and r. Let s2 be
one of them; then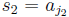 
for some index j2 > j1.
Excluding the numbers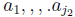 
, there
is a rational number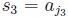 
with j3 > j2
between
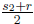and r. Continuing in that way, we
produce an increasing subsequence
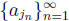that converges to r.
(b). Find a subsequence of the rational number sequence
0, 1, 1/2, 1/3, 2/3, 1/4, 3/4, 1/5.2/5, 3/5, 4/5, ... that converges to 2/3.
Solution: Consider the sequence
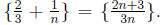Those fractions are in lowest terms
except when 3 divides n. Take the subsequence of that sequence obtained by
leaving out the
terms whose indices are divisible by 3. Then that subsequence is also a
subsequence of the
sequence 0, 1, 1/2, 1/3, 2/3, 1/4, 3/4, 1/5.2/5, 3/5, 4/5, ..., and it converges
to 2/3.
3. The ordered set of real numbers has the property that each bounded set of
real numbers
has a greatest lower bound and a least upper bound.
Let
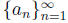be an increasing bounded sequence of real numbers, and let m be the least upper
bound of the (bounded) set of numbers in the sequence, Show that the sequence
converges
to m.
Solution: We need to show that for each value ε
> 0, there is an index Nε such that
for n ≥ Nε, |m − an| < ε. Since each an≤m, the condition |m − an| < ε is the
condition
m−an < ε. Because the sequence is increasing, if we find an index Nε
such that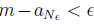 
,
then m−an < ε for n≥Nε, automatically, i.e., when the sequence is increasing, if
one term
gets within ε of m, then all subsequence terms are also within ε of m.
Because m is the least upper bound for the terms of the
sequence, m − ε is not an upper
bound. Hence, there is a term an of the sequence such that m − ε < an,
i.e., m − an< ε.
Denote that index n by the symbol Nε. Then,
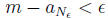as required.
It is a fact that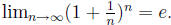 
Using that fact, show the facts given in exercise 4.
4(a). Compute that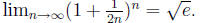 
Solution: Because
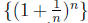converges to e, the subsequence
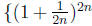also converges to
e. So,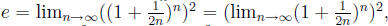 
by problem 5 below (which gives the
formula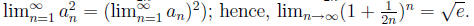 
(b). Compute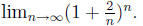 
Solution: The sequence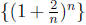 
is increasing, just as the sequence that converges to e is
increasing. Hence, it has the same limit as any infinite subsequence by problem
1. Consider
the subsequence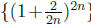 
where we just use the even
indices. That subsequence converges
to the limit e^2, since it is the sequence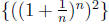 
which converges to e^2, using problem 5
again.
(c). Compute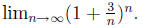 
Solution: Just as in part (b), the sequence converges to e^3
Showing that a sequence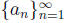 
has limit m is the same as showing that the sequence
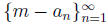has limit 0.
5. Suppose that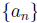 
converges to m and that 
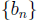converges to k. Show
that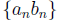 
converges to mk. (Hint: Show that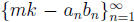 
converges
to 0. To do that, write
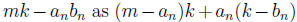and show that each of the summands in that
expression
converges to 0 as n goes to 
).
Solution: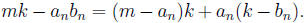
Let us
show that each summand converges
to 0. Since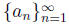 
converges to m, the sequence
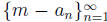converges to 0. Since k
is a constant, the sequence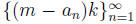 
also converges
to 0. Consider the summand
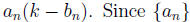converges, the set of terms in the sequence
has an upper bound M.
Then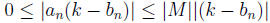 
where the sequence
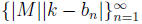converges to 0;
hence, the sequence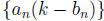 
also converges to 0, by
the preceding inequality.
6. Show that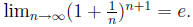 
(Use
problem 5).
Solution: Consider the product sequence
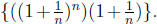Since the first sequence in the
product converges to e and the second sequence in the product converges to 1,
the product
converges to (e)(1) = e.